题目内容
定义:离心率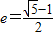 的椭圆为“黄金椭圆”,已知椭圆E:
的椭圆为“黄金椭圆”,已知椭圆E: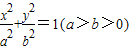 的一个焦点为F(c,0),p为椭圆E上任意一点.
的一个焦点为F(c,0),p为椭圆E上任意一点.(1)试证:若a、b、c不是等比数列,则E一定不是“黄金椭圆”;
(2)若E为黄金椭圆;问:是否存在过点F,P的直线l;使l与y轴的交点R满足
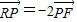 ;若存在,求直线l的斜率K;若不存在,说明理由.
;若存在,求直线l的斜率K;若不存在,说明理由.
【答案】分析:(1)假设E为黄金椭圆,则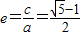 ,根据等比中项的性质可推断a、b、c成等比数列,与已知矛盾,故原命题成立.
,根据等比中项的性质可推断a、b、c成等比数列,与已知矛盾,故原命题成立.
(2)设直线l的方程为y=k(x-c),进而可表示出R的坐标根据及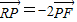 ,进而表示出P的坐标,把P点代入椭圆的方程整理后可解得k存在,求出k.
,进而表示出P的坐标,把P点代入椭圆的方程整理后可解得k存在,求出k.
解答:解:(1)证明:假设E为黄金椭圆,则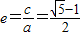 ,即
,即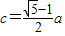
∴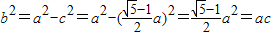
即a,b,c成等比数列,与已知矛盾
故原命题成立.
(2)依题意设直线l的方程为y=k(x-c)
令x=0,有y=-kc,即R(0,-kc)
点F(c,0),设P(x,y)
则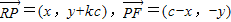
∵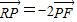
∴x=2(c-x)
即p(2c,kc)
y+kc=2y
∵P在椭圆上∴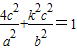
又b2=ac∴4e2+k2e=1
故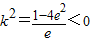 ,与k2≥0矛盾
,与k2≥0矛盾
所以,满足题意的直线不存在.
点评:本题主要考查了椭圆的简单性质,注意寻找黄金双曲线中a,b,c之间的关系,利用椭圆的性质求解,属中档题.
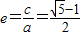 ,根据等比中项的性质可推断a、b、c成等比数列,与已知矛盾,故原命题成立.
,根据等比中项的性质可推断a、b、c成等比数列,与已知矛盾,故原命题成立.(2)设直线l的方程为y=k(x-c),进而可表示出R的坐标根据及
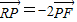 ,进而表示出P的坐标,把P点代入椭圆的方程整理后可解得k存在,求出k.
,进而表示出P的坐标,把P点代入椭圆的方程整理后可解得k存在,求出k.解答:解:(1)证明:假设E为黄金椭圆,则
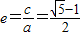 ,即
,即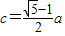
∴
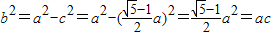
即a,b,c成等比数列,与已知矛盾
故原命题成立.
(2)依题意设直线l的方程为y=k(x-c)
令x=0,有y=-kc,即R(0,-kc)
点F(c,0),设P(x,y)
则
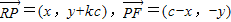
∵
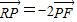
∴x=2(c-x)
即p(2c,kc)
y+kc=2y
∵P在椭圆上∴
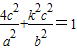
又b2=ac∴4e2+k2e=1
故
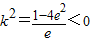 ,与k2≥0矛盾
,与k2≥0矛盾所以,满足题意的直线不存在.
点评:本题主要考查了椭圆的简单性质,注意寻找黄金双曲线中a,b,c之间的关系,利用椭圆的性质求解,属中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
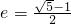 的椭圆为“黄金椭圆”,已知椭圆
的椭圆为“黄金椭圆”,已知椭圆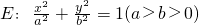 的一个焦点为F(c,0)(c>0),P为椭圆E上的任意一点.
的一个焦点为F(c,0)(c>0),P为椭圆E上的任意一点.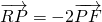 ?若存在,求直线l的斜率k;若不存在,请说明理由;
?若存在,求直线l的斜率k;若不存在,请说明理由;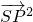 取最大值时点P的坐标.
取最大值时点P的坐标.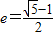 的椭圆为“黄金椭圆”,已知椭圆
的椭圆为“黄金椭圆”,已知椭圆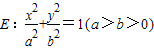 的两个焦点分别为F1(-c,0)、F2(c,0)(c>0),P为椭圆E上的任意一点.
的两个焦点分别为F1(-c,0)、F2(c,0)(c>0),P为椭圆E上的任意一点.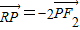 ?若存在,求直线l的斜率k;若不存在,请说明理由;
?若存在,求直线l的斜率k;若不存在,请说明理由;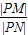 的值.
的值.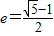 的椭圆为“黄金椭圆”,已知椭圆
的椭圆为“黄金椭圆”,已知椭圆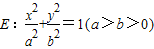 的一个焦点为F(c,0)(c>0),P为椭圆E上的任意一点.
的一个焦点为F(c,0)(c>0),P为椭圆E上的任意一点.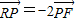 ?若存在,求直线l的斜率k;若不存在,请说明理由;
?若存在,求直线l的斜率k;若不存在,请说明理由;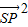 取最大值时点P的坐标.
取最大值时点P的坐标.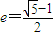 的椭圆为“黄金椭圆”,已知E:
的椭圆为“黄金椭圆”,已知E: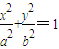 (a>b>0)的一个焦点为F(c,0)(c>0),则E为“黄金椭圆”是a,b,c成等比数列的( )
(a>b>0)的一个焦点为F(c,0)(c>0),则E为“黄金椭圆”是a,b,c成等比数列的( )