题目内容
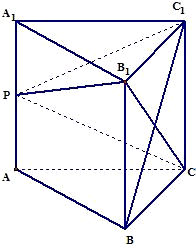 正三棱柱ABC-A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.
正三棱柱ABC-A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.
(1)求正三棱柱ABC-A1B1C1的体积;
(2)判断直线B1P与平面ACC1A1是否垂直,请证明你的结论;
(3)当BC1⊥B1P时,求二面角C-B1P-C1的余弦值.
解:(1)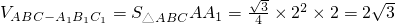 ,
,
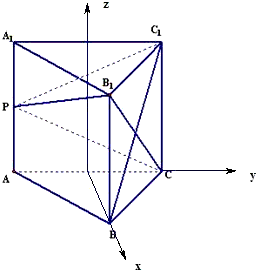
(2)建立如图空间坐标系O-xyz,设AP=a,
则A,C,B1,P的坐标分别为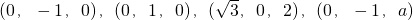 ;
;
∴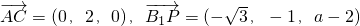
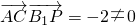 ,
,
∴B1P不垂直AC;
∴直线B1P不可能与平面ACC1A1垂直;
 (3)
(3)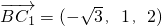 ,
,
由BC1⊥B1P,得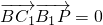 ,
,
即2+2(a-2)=0∴a=1;
又BC1⊥B1C∴BC1⊥面CB1P;
∴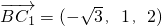 是面CB1P的法向量;
是面CB1P的法向量;
设面C1B1P的法向量为 ,
,
由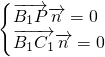 得
得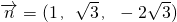 ,
,
设二面角C-B1P-C1的大小为α,则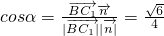 ,
,
∴二面角C-B1P-C1的余弦值大小为 .
.
分析:1、根据公式求解即可.2、利用空间直角坐标系,根据向量可以证明.3、借用(2)中的坐标系,利用法向量求解.
点评:本题考查学生的空间想象能力,空间直角坐标系的使用,及二面角的求法,是中档题.
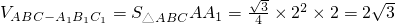 ,
,(2)建立如图空间坐标系O-xyz,设AP=a,
则A,C,B1,P的坐标分别为
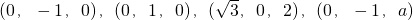 ;
;∴
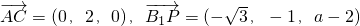
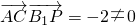 ,
,∴B1P不垂直AC;
∴直线B1P不可能与平面ACC1A1垂直;
 (3)
(3)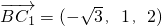 ,
,由BC1⊥B1P,得
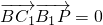 ,
,即2+2(a-2)=0∴a=1;
又BC1⊥B1C∴BC1⊥面CB1P;
∴
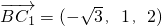 是面CB1P的法向量;
是面CB1P的法向量;设面C1B1P的法向量为
 ,
,由
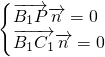 得
得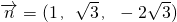 ,
,设二面角C-B1P-C1的大小为α,则
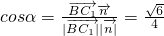 ,
,∴二面角C-B1P-C1的余弦值大小为
 .
.分析:1、根据公式求解即可.2、利用空间直角坐标系,根据向量可以证明.3、借用(2)中的坐标系,利用法向量求解.
点评:本题考查学生的空间想象能力,空间直角坐标系的使用,及二面角的求法,是中档题.

练习册系列答案
相关题目
 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 如图在 正三棱柱ABC-A1 B1 C1中,底面边长为
如图在 正三棱柱ABC-A1 B1 C1中,底面边长为 如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a. =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.