题目内容
若向量 =(cosα,sinβ),
=(cosα,sinβ), =(cosα,sinβ),则
=(cosα,sinβ),则 与
与 一定满足
一定满足
- A.
 与
与 的夹角等于α-β
的夹角等于α-β - B.
 ⊥
⊥
- C.
 ∥
∥
- D.(
 +
+ )⊥(
)⊥( -
- )
)
D
分析:欲求 与
与 满足的关系,先利用平面向量积的公式,判断
满足的关系,先利用平面向量积的公式,判断 与
与 是否有垂直或者平行的关系,再判断各个选项中的关系是否满足.
是否有垂直或者平行的关系,再判断各个选项中的关系是否满足.
解答:因为 =cos(α-β),这表明这两个向量的夹角的余弦值为cos(α-β),但不标明两向量夹角为α-β.
=cos(α-β),这表明这两个向量的夹角的余弦值为cos(α-β),但不标明两向量夹角为α-β.
同时,也不能得出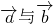 的平行和垂直关系.
的平行和垂直关系.
因为计算得到( +
+ )•(
)•( -
- )=0,所以(
)=0,所以( +
+ )⊥(
)⊥( -
- ).
).
故选D.
点评:本题考查平面向量的综合知识,考查平面向量积的运算用于判别向量间的关系.
分析:欲求
 与
与 满足的关系,先利用平面向量积的公式,判断
满足的关系,先利用平面向量积的公式,判断 与
与 是否有垂直或者平行的关系,再判断各个选项中的关系是否满足.
是否有垂直或者平行的关系,再判断各个选项中的关系是否满足.解答:因为
 =cos(α-β),这表明这两个向量的夹角的余弦值为cos(α-β),但不标明两向量夹角为α-β.
=cos(α-β),这表明这两个向量的夹角的余弦值为cos(α-β),但不标明两向量夹角为α-β.同时,也不能得出
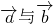 的平行和垂直关系.
的平行和垂直关系.因为计算得到(
 +
+ )•(
)•( -
- )=0,所以(
)=0,所以( +
+ )⊥(
)⊥( -
- ).
).故选D.
点评:本题考查平面向量的综合知识,考查平面向量积的运算用于判别向量间的关系.

练习册系列答案
相关题目
若向量
=(cosα,sinα),
=(cosβ,sinβ),则
与
一定满足( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、(
| ||||||||
C、
| ||||||||
D、
|
若向量
=(cosα,sinβ),
=(cosα,sinβ),则
与
一定满足( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、(
|