题目内容
已知f(n)=cos
(n∈N*),则f(1)+f(2)+f(3)+…+f(100)=______.
| nπ |
| 4 |
当n-1时,f(1)=cos
=
,当n=2时,f(2)=cos
=cos
=0,当n=3时,f(3)=cos
=-
,当n=4时,f(4)=cos
=cosπ=-1,
当n=5时,f(5)=cos
=cos(π+
)=-
,当n=6时,f(6)=cos
=cos(π+
)=0,当n=7时,f(7)=cos
=cos(π+
)=
,
当n=8时,f(8)=cos
=cos2π=1,当n=9时,f(9)=cos
=cos(2π+
)=cos
=
,…由以上数值出现的规律可以知道,此函数的一个周期为T=8,
利用函数的周期性,而f(1)+f(2)+f(3)+…f(8)=0,则f(1)+f(2)+f(3)+…+f(100)=f(1)+F(2)+f(3)+f(4)=
+0+(-
)+(-1)=-1.
故答案为:-1.
| π |
| 4 |
| ||
| 2 |
| 2π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| ||
| 2 |
| 4π |
| 4 |
当n=5时,f(5)=cos
| 5π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 6π |
| 4 |
| 2π |
| 4 |
| 7π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
当n=8时,f(8)=cos
| 8π |
| 4 |
| 9π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
利用函数的周期性,而f(1)+f(2)+f(3)+…f(8)=0,则f(1)+f(2)+f(3)+…+f(100)=f(1)+F(2)+f(3)+f(4)=
| ||
| 2 |
| ||
| 2 |
故答案为:-1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (n∈N*),则f(1)+f(2)+f(3)+…+f(100)=________.
(n∈N*),则f(1)+f(2)+f(3)+…+f(100)=________.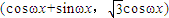 ,n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m•n,且f(x)的对称中心到f(x)对称轴的最近距离不小于
,n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m•n,且f(x)的对称中心到f(x)对称轴的最近距离不小于