题目内容
关于平面向量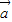 ,
, ,
, ,有下列几个命题:
,有下列几个命题:①若
 ,则
,则 或
或 ;
;②若
 与
与 均为单位向量,它们的夹角为60°,则
均为单位向量,它们的夹角为60°,则 ;
;③若非零向量
 ,
, ,
, 满足
满足 ,
, ,则
,则 与
与 的夹角为120°;
的夹角为120°;④若
 ,
, ,则
,则 在
在 方向上的投影是-1.
方向上的投影是-1.其中正确的是 .(请将所有正确命题的序号都填上)
【答案】分析:根据向量的乘法不满足消去率,可知①不正确;利用向量的数量积公式,可得结论;非零向量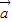 ,
,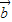 ,
,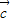 满足
满足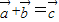 ,可得
,可得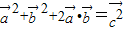 ,从而可得结论;利用
,从而可得结论;利用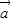 在
在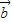 方向上的投影是
方向上的投影是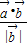 ,即可得出结论.
,即可得出结论.
解答:解:根据向量的乘法不满足消去率,可知①不正确;
∵ 与
与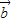 均为单位向量,它们的夹角为60°,∴
均为单位向量,它们的夹角为60°,∴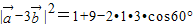 =7,∴
=7,∴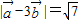 ;
;
,即②正确;
∵非零向量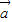 ,
,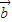 ,
,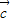 满足
满足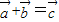 ,∴
,∴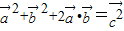 ,∵
,∵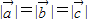 ,∴
,∴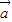 与
与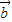 的夹角为120°,即③正确;
的夹角为120°,即③正确;
∵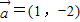 ,
,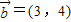 ,∴
,∴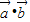 =-5,
=-5,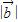 =5,∴
=5,∴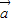 在
在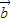 方向上的投影是
方向上的投影是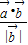 =-1,即④正确
=-1,即④正确
故答案为:②③④.
点评:本题考查命题真假的判断,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.
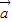 ,
,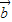 ,
,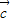 满足
满足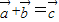 ,可得
,可得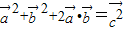 ,从而可得结论;利用
,从而可得结论;利用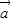 在
在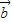 方向上的投影是
方向上的投影是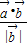 ,即可得出结论.
,即可得出结论.解答:解:根据向量的乘法不满足消去率,可知①不正确;
∵
 与
与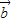 均为单位向量,它们的夹角为60°,∴
均为单位向量,它们的夹角为60°,∴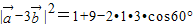 =7,∴
=7,∴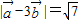 ;
;,即②正确;
∵非零向量
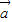 ,
,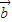 ,
,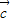 满足
满足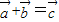 ,∴
,∴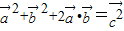 ,∵
,∵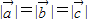 ,∴
,∴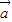 与
与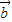 的夹角为120°,即③正确;
的夹角为120°,即③正确;∵
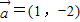 ,
,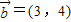 ,∴
,∴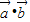 =-5,
=-5,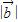 =5,∴
=5,∴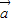 在
在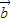 方向上的投影是
方向上的投影是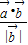 =-1,即④正确
=-1,即④正确故答案为:②③④.
点评:本题考查命题真假的判断,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 ,
, ,
, .有下列三个命题:
.有下列三个命题: •
• =
= •
• ,则
,则 =
= .
. =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°. ,
, ,
, ,有下列三个命题:
,有下列三个命题: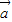 •
• =
= •
• ,则
,则 =
= 、
、 =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=|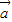 -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°. ,
, ,
, ,有下列三个命题:
,有下列三个命题: •
• =
= •
• ,则
,则 =
= 、
、 =(1,k),
=(1,k),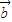 =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°. ,
, ,
, ,有下列三个命题:
,有下列三个命题: •
• =
= •
• ,则
,则 =
= 、
、 =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.