题目内容
设 成等比数列,其公比为2,则
成等比数列,其公比为2,则 的值为( )
的值为( )
A. | B. | C. | D.1 |
A
解析试题分析:根据题意,由于设 成等比数列,其公比为2,则
成等比数列,其公比为2,则 ,因此可知
,因此可知 ,故选A.
,故选A.
考点:等比数列
点评:解决该试题的关键是利用等比数列的性质来得到整体之间的关系,进而得到结论,运用公比表示,属于基础题。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
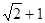 与
与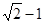 的等比中项是( )
的等比中项是( )
| A.1 | B.-1 | C.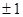 | D.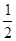 |
等比数列{ }中,若
}中,若 ,则
,则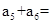 ( )
( )
| A.2 | B.40 | C.80 | D.120 |
在等比数列{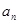 }中,若
}中,若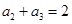 ,
,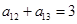 ,则
,则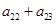 的值是( )
的值是( )
A.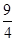 | B.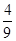 | C.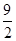 | D.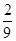 |
已知等比数列{an}公比为q,其前n项和为Sn,若S3,S9,S6成等差数列,则q3等于
A.- | B.1 | C.- 或1 或1 | D.-1或 |
已知等比数列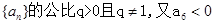 ,则 ( )
,则 ( )
A.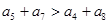 | B.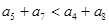 |
C.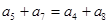 | D.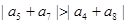 |
等比数列{an}中,a7=10,q=-2,则a10 =( )
| A.4 | B.40 | C.80 | D.-80 |
已知数列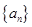 是各项均为正数且公比不等于
是各项均为正数且公比不等于 的等比数列.对于函数
的等比数列.对于函数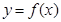 ,若数列
,若数列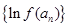 为等差数列,则称函数
为等差数列,则称函数 为“保比差数列函数”.现有定义在
为“保比差数列函数”.现有定义在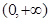 上的如下函数:①
上的如下函数:①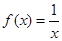 , ②
, ②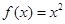 , ③
, ③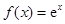 , ④
, ④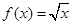 ,
,
则为“保比差数列函数”的所有序号为( )
| A.①② | B.③④ | C.①②④ | D.②③④ |
数列 满足
满足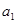 ,
,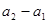 ,
, ,…,
,…,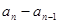 是首项为
是首项为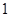 ,公比为
,公比为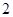 的等比数列,那么
的等比数列,那么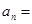 ( )
( )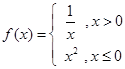
A.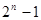 | B.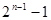  | C.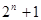 | D.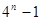 |