题目内容
已知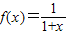 ,各项均为正数的数列{an}满足a1=1,an+2=f(an),若a2010=a2012,则a20+a11的值是 .
,各项均为正数的数列{an}满足a1=1,an+2=f(an),若a2010=a2012,则a20+a11的值是 .
【答案】分析:根据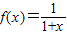 ,各项均为正数的数列{an}满足a1=1,an+2=f(an),可确定a1=1,
,各项均为正数的数列{an}满足a1=1,an+2=f(an),可确定a1=1,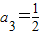 ,
,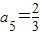 ,a7=
,a7= ,
,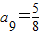 ,
,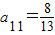 ,利用a2010=a2012,可得a2010=
,利用a2010=a2012,可得a2010=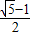 (负值舍去),依次往前推得到a20=
(负值舍去),依次往前推得到a20=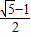 ,由此可得结论.
,由此可得结论.
解答:解:∵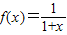 ,各项均为正数的数列{an}满足a1=1,an+2=f(an),
,各项均为正数的数列{an}满足a1=1,an+2=f(an),
∴a1=1,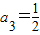 ,
,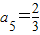 ,a7=
,a7= ,
,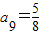 ,
,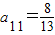
∵a2010=a2012,
∴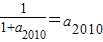
∴a2010=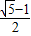 (负值舍去),由a2010=
(负值舍去),由a2010=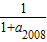 得a2008=
得a2008=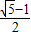 …
…
依次往前推得到a20=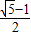
∴a20+a11=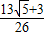
故答案为: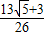
点评:本题主要考查数列的概念、组成和性质、同时考查函数的概念.理解条件an+2=f(an),是解决问题的关键,本题综合性强,运算量较大,属于中高档试题.
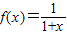 ,各项均为正数的数列{an}满足a1=1,an+2=f(an),可确定a1=1,
,各项均为正数的数列{an}满足a1=1,an+2=f(an),可确定a1=1,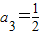 ,
,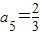 ,a7=
,a7= ,
,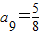 ,
,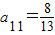 ,利用a2010=a2012,可得a2010=
,利用a2010=a2012,可得a2010=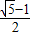 (负值舍去),依次往前推得到a20=
(负值舍去),依次往前推得到a20=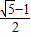 ,由此可得结论.
,由此可得结论.解答:解:∵
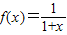 ,各项均为正数的数列{an}满足a1=1,an+2=f(an),
,各项均为正数的数列{an}满足a1=1,an+2=f(an),∴a1=1,
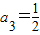 ,
,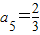 ,a7=
,a7= ,
,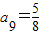 ,
,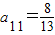
∵a2010=a2012,
∴
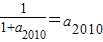
∴a2010=
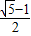 (负值舍去),由a2010=
(负值舍去),由a2010=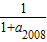 得a2008=
得a2008=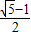 …
…依次往前推得到a20=
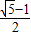
∴a20+a11=
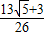
故答案为:
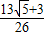
点评:本题主要考查数列的概念、组成和性质、同时考查函数的概念.理解条件an+2=f(an),是解决问题的关键,本题综合性强,运算量较大,属于中高档试题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ,各项均为正数的数列
,各项均为正数的数列 满足
满足 ,若
,若 ,则
,则 .
. 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 ,
, ;
; ,求数列
,求数列 的前
的前 项和
项和 .
.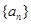 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且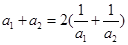 ,
,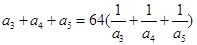
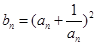 ,求数列
,求数列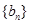 的前
的前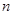 项和
项和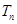 。
。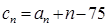 ,求数列{
,求数列{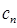 }的前
}的前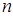 项和最小时
项和最小时 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 ,
,
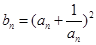 ,求数列
,求数列 的前
的前 项和
项和 。
。