题目内容
6.已知f(x)=log2(1+x4)-$\frac{1+mx}{1+{x}^{2}}$(x∈R)是偶数,求实常数m的值,并给出函数f(x)的单调区间(不要求证明)分析 由偶函数的定义,取特殊值得关于m的方程f(-1)=f(1),解得m=0,最后检验所求出的值符合题意;
解答 解:由题意得:f(-1)=1-$\frac{1+m}{2}$,f(1)=1-$\frac{1+m}{2}$.
函数为偶函数,所以f(-1)=f(1),解得m=0.
检验:当m=0时,f(x)=log2(1+x4)-$\frac{1}{1+{x}^{2}}$,f(-x)=f(x)成立,函数为偶函数.
函数在区间(-∞,0)上是减函数,在区间(0,+∞)上是增函数.
点评 考查了函数的单调性与奇偶性,同时考查了含有参数的不等式的求解,属于中档题.

练习册系列答案
相关题目
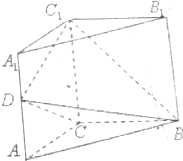 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.