题目内容
已知数列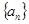 中,
中,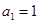 ,且当
,且当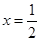 时,函数
时,函数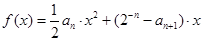 取得极值。
取得极值。
(1)若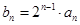 ,求数列
,求数列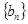 的通项公式;
的通项公式;
(2)设数列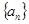 的前
的前 项和为
项和为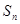 ,试证明:
,试证明: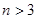 时,
时,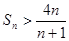 .
.
【答案】
(1)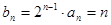
(2)证明略
【解析】解:(1)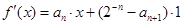 ……1分
……1分
由题意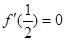 得
得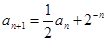
由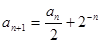 得
得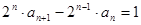 ……3分
……3分
又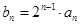
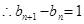
所以数列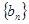 是首项为
是首项为 、公差为
、公差为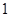 的等差数列
……4分
的等差数列
……4分
所以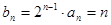 ……5分
……5分
(2) 由(1)可得  ……6分
……6分
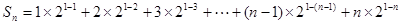
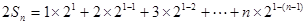
两式相减得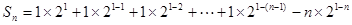 ……8分
……8分
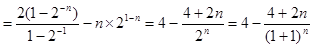 ……9分
……9分
据二项式定理得
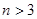 时,
时,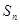
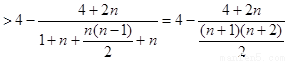
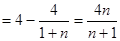 …12分.
…12分.

练习册系列答案
相关题目
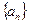 中,
中,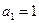 ,且当
,且当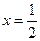 时,函数
时,函数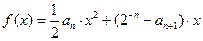 取得极值。
取得极值。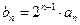 ,求数列
,求数列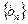 的通项公式;
的通项公式;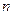 项和为
项和为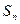 ,试证明:
,试证明: 时,
时,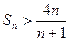 .
.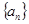 中,
中,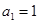 ,且当
,且当 时,函数
时,函数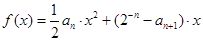
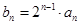 ,证明数列
,证明数列 为等差数列;
为等差数列;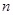 项和为
项和为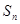 ,求
,求  中,
中, ,且当
,且当 时,函数
时,函数 取得极值。
取得极值。 满足:
满足: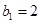 ,
, ,证明:
,证明: 是等差数列,并求数列
是等差数列,并求数列 项和
项和 .
. 中,
中, ,且当
,且当 时,函数
时,函数 取得极值。
取得极值。 ,求数列
,求数列 的通项公式;
的通项公式; 项和为
项和为 ,试证明:
,试证明: 时,
时, .
.