题目内容
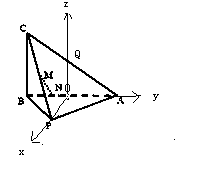
【题目】如图,在三棱锥C﹣PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB. 
(1)求AN的长;
(2)求锐二面角P﹣NC﹣A的余弦值.
【答案】
(1)解:如图,分别取AB,AC的中点O,Q,连接OP,OQ,
以O为原点,以OP为x轴,以OA为y轴,以OQ为z轴,
建立空间直角坐标系,
则由题意知:A(0,3,0),B(0,﹣3,0),
P(4,0,0),C(0,﹣3,4),
M(2,﹣ ![]() ,2),N(0,t,0).
,2),N(0,t,0).
![]() =
= ![]() ,
, ![]() =(0,6,0).
=(0,6,0).
∵ ![]() ⊥
⊥ ![]() ,∴
,∴ ![]()
![]() =
= ![]() =0,解得t=﹣
=0,解得t=﹣ ![]() ,
,
∴AN=3﹣ ![]() =
= ![]() .
.
(2)解:N ![]() ,∴
,∴ ![]() =
= ![]() ,
, ![]() =(2,0,2),
=(2,0,2),
设平面MNC的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 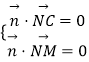 ,即
,即 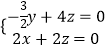 ,则取
,则取 ![]() =(﹣3,8,3),
=(﹣3,8,3),
平面ANC的一个法向量为 ![]() =(1,0,0),
=(1,0,0),
cos ![]() =
= ![]() =
= ![]() =﹣
=﹣ ![]() .
.
∴锐二面角P﹣NC﹣A的余弦值为 ![]() .
.
【解析】(1)如图,分别取AB,AC的中点O,Q,连接OP,OQ,以O为原点,以OP为x轴,以OA为y轴,以OQ为z轴,建立空间直角坐标系,设N(0,t,0).由 ![]() ⊥
⊥ ![]() ,可得
,可得 ![]()
![]() =0,解得t,即可得出AN.(2)设平面MNC的一个法向量为
=0,解得t,即可得出AN.(2)设平面MNC的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则 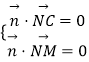 ,可得
,可得 ![]() ,平面ANC的一个法向量为
,平面ANC的一个法向量为 ![]() =(1,0,0),利用cos
=(1,0,0),利用cos ![]() =
= ![]() 即可得出.
即可得出.
【考点精析】本题主要考查了棱锥的结构特征的相关知识点,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方才能正确解答此题.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |
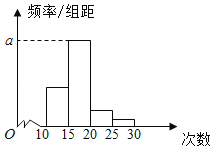
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
