题目内容
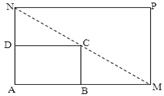
如图所示,将一矩形花坛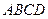 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛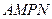 ,要求
,要求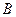 点在
点在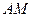 上,
上,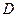 点在
点在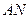 上,且对角线
上,且对角线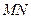 过
过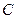 点,已知
点,已知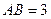 米,
米,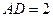 米.
米.
(I)要使矩形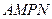 的面积大于32平方米,则
的面积大于32平方米,则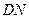 的长应在什么范围内?
的长应在什么范围内?
(II)当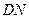 的长度是多少时,矩形花坛
的长度是多少时,矩形花坛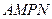 的面积最小?并求出最小值
的面积最小?并求出最小值
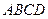 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛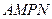 ,要求
,要求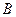 点在
点在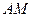 上,
上,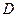 点在
点在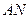 上,且对角线
上,且对角线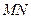 过
过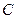 点,已知
点,已知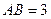 米,
米,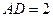 米.
米.
(I)要使矩形
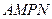 的面积大于32平方米,则
的面积大于32平方米,则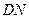 的长应在什么范围内?
的长应在什么范围内?(II)当
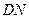 的长度是多少时,矩形花坛
的长度是多少时,矩形花坛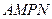 的面积最小?并求出最小值
的面积最小?并求出最小值(I)
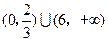 (II)
(II) 的长度是
的长度是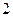 米时,最小值为
米时,最小值为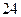 平方米
平方米(I)设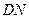 的长为
的长为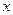 (
(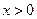 )米,则
)米,则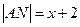 米
米
∵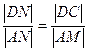 ,∴
,∴ , ……………………2分
, ……………………2分
∴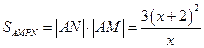
由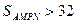 得
得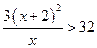 ,
,
又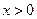 ,得
,得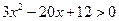 ,
,
解得: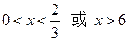
即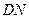 长的取值范围是
长的取值范围是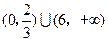 ……………………7分
……………………7分
(II)矩形花坛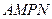 的面积为
的面积为
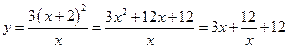
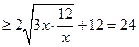 ……………………10分
……………………10分
当且仅当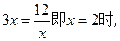 矩形花坛
矩形花坛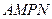 的面积取得最小值
的面积取得最小值 .
.
故,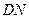 的长度是
的长度是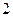 米时,矩形
米时,矩形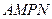 的面积最小,最小值为
的面积最小,最小值为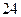 平方米.…12分
平方米.…12分
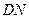 的长为
的长为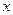 (
(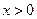 )米,则
)米,则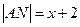 米
米∵
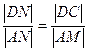 ,∴
,∴ , ……………………2分
, ……………………2分∴
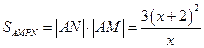
由
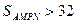 得
得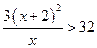 ,
,又
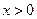 ,得
,得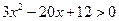 ,
,解得:
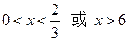
即
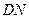 长的取值范围是
长的取值范围是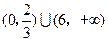 ……………………7分
……………………7分(II)矩形花坛
 的面积为
的面积为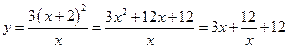
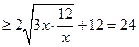 ……………………10分
……………………10分当且仅当
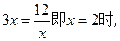 矩形花坛
矩形花坛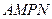 的面积取得最小值
的面积取得最小值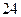 .
.故,
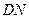 的长度是
的长度是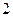 米时,矩形
米时,矩形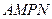 的面积最小,最小值为
的面积最小,最小值为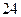 平方米.…12分
平方米.…12分
练习册系列答案
相关题目
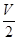
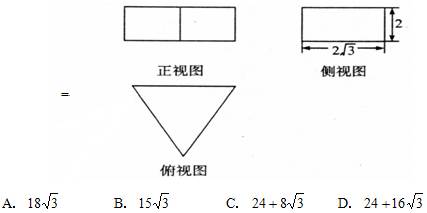
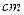 )则该组合体的体积为( )
)则该组合体的体积为( )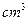
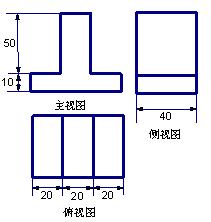

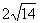 ,则这个长方体的体积是( )
,则这个长方体的体积是( )  cm、
cm、 cm,侧棱长为
cm,侧棱长为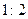 ,则其外接圆的面积比为
,则其外接圆的面积比为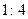 ;类似地,空间中,两个正四面体的棱长比为
;类似地,空间中,两个正四面体的棱长比为 .
.