题目内容
已知函数f(x)=ax-(1)求a的值;
(2)设0<a1<![]() ,an+1=f(an),n∈N*,证明:an<
,an+1=f(an),n∈N*,证明:an<![]() .
.
思路分析:在用数学归纳法证明不等式的过程中,充分利用了数列递推关系式an+1=f(an)=![]() a2n+an的函数单调性,需注意命题的递推关系式中起点位置的推移.
a2n+an的函数单调性,需注意命题的递推关系式中起点位置的推移.
(1)解:由于f(x)=ax![]() x2的最大值不大于
x2的最大值不大于![]() ,所以
,所以
f(![]() )=
)=![]() ≤
≤![]() ,即a2≤1.
,即a2≤1.
又x∈[![]() ,
,![]() ]时f(x)≥
]时f(x)≥![]() ,
,
所以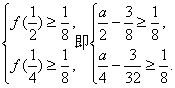 解得a≥1.
解得a≥1.
∴a=1.
(2)证明:(Ⅰ)当n=1时,0<a1<![]() ,不等式0<an<
,不等式0<an<![]() 成立;
成立;
因f(x)>0,x∈(0,![]() ),所以0<a2=f(a1)≤
),所以0<a2=f(a1)≤![]() <
<![]() ,
,
故n=2时不等式也成立.
(Ⅱ)假设n=k(k≥2)时,不等式0<ak<![]() 成立,
成立,
因为f(x)=x-![]() x2的对称轴为x=
x2的对称轴为x=![]() ,知f(x)在[0,
,知f(x)在[0,![]() ]为增函数,所以由0<ak<
]为增函数,所以由0<ak<![]() ≤
≤![]() 得0<f(ak)<f(
得0<f(ak)<f(![]() ),于是有
),于是有
0<ak+1<![]() -
-![]() ·
·![]() .
.
所以当n=k+1时,不等式也成立.
根据(Ⅰ)(Ⅱ)可知,对任何n∈N*,不等式an<![]() 成立.
成立.
方法归纳
将起点的位置推移至2的目的,就是要将ak和![]() 置于函数f(x)的单调区间[0,
置于函数f(x)的单调区间[0,![]() ]内,从而由0<ak<
]内,从而由0<ak<![]() ≤
≤![]() 得0<f(ak)<f(
得0<f(ak)<f(![]() ).
).

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |