题目内容
已知圆锥的表面积为3π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径是
1
1
.分析:设出圆锥的底面半径,由它的侧面展开图是一个半圆,分析出母线与半径的关系,结合圆锥的表面积为3π,构造方程,可求出半径
解答:解:设圆锥的底面的半径为r,圆锥的母线为l,
则由πl=2πr得l=2r,
而S=πr2+πr•2r=3πr2=3π
故r2=1
解得r=1
故答案为:1
则由πl=2πr得l=2r,
而S=πr2+πr•2r=3πr2=3π
故r2=1
解得r=1
故答案为:1
点评:本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
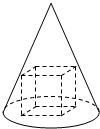 已知圆锥的母线长与底面半径长之比为3:1,一个正方体有四个顶点在圆锥的底面内,另外的四个顶点在圆锥的侧面上(如图),则圆锥与正方体的表面积之比为( )
已知圆锥的母线长与底面半径长之比为3:1,一个正方体有四个顶点在圆锥的底面内,另外的四个顶点在圆锥的侧面上(如图),则圆锥与正方体的表面积之比为( )| A、π:1 | B、3π:1 | C、3π:2 | D、3π:4 |