题目内容
(2013•临沂一模)已知函数f(x)=cos(x-
)-sin(
-x).
(I)求函数f(x)的最小正周期;
(Ⅱ)若α∈(0,
),且f(α+
)=
,求f(2α)的值.
| π |
| 3 |
| π |
| 2 |
(I)求函数f(x)的最小正周期;
(Ⅱ)若α∈(0,
| π |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
分析:(I)利用两角和的正弦公式化简函数f(x)的解析式为sin(x-
),由此求得它的最小正周期的值;
(II)先由f(α+
)=
可以求出sinα的值,进而得出cosα、cos2α、sin2α的值,然后即可求出f(2α).
| π |
| 6 |
(II)先由f(α+
| π |
| 6 |
| 3 |
| 5 |
解答:解:(I)f(x)=cos(x-
)-sin(
-x)=
cosx+
sinx-cosx=
sinx-
cosx=sin(x-
)
∴f(x)的最小正周期为2π
(II)由(I)知f(x)=sin(x-
)
所以f(α+
)=sin(α+
-
)=sinα=
∵α∈(0,
),
∴cosα=
=
∴sin2α=2sinαcosα=2×
×
=
cos2α=2cos2α-1=2×(
)2-1=
∴f(2α)=sin(2α-
)=
sin2α-
cos2α=
×
-
×
=
| π |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴f(x)的最小正周期为2π
(II)由(I)知f(x)=sin(x-
| π |
| 6 |
所以f(α+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 5 |
∵α∈(0,
| π |
| 2 |
∴cosα=
| 1-sin2α |
| 4 |
| 5 |
∴sin2α=2sinαcosα=2×
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
cos2α=2cos2α-1=2×(
| 4 |
| 5 |
| 7 |
| 25 |
∴f(2α)=sin(2α-
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 24 |
| 25 |
| 1 |
| 2 |
| 7 |
| 25 |
24
| ||
| 50 |
点评:此题考查了诱导公式、两角和与差公式,熟练掌握相关公式是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
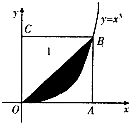 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )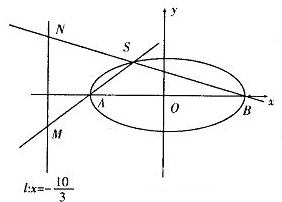 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: