题目内容
(本题满分16分)已知函数f(x)对任意实数x均有f(x)=k f(x+2),其中常数k为负数,且f(x)在区间[0,2]有表达式f(x)=x(x-2)。
⑴求f(-1),f(2.5)的值(用k表示);
⑵写出f(x)在[-3,2]上的表达式,并讨论f(x)在[-3,2]上的单调性(不要证明);
⑶求出f(x)在[-3,2]上最小值与最大值,并求出相应的自变量的取值。
⑴f(-1)= k f(1)= k(-1)=-k …………………………………………2′
f(2.5)=![]() f(0.5)=
f(0.5)=![]() ×
×![]() ×(-
×(-![]() )=-
)=-![]() …………………………4′
…………………………4′
x∈[-2,0]时,x+2∈[0,2]
∴ f(x)= k f(x+2)= k(x+2)x …………………………………………6′
x∈[-3,-2)时 x+2∈[-1,0)
∴ f(x)= k f(x+2)= k2(x+4)(x+2)……………………………………8′
∴ f(x)=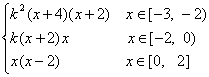
⑵f(x)在[-3,-1]上单调增,在[1, 2] 单调增
在[-1, 1]上单调减 ……………………………………………………12′
⑶x=-1,f(x)max=-k ……………………………………………………13′
k=-1,f(x)min=-1,此时x=1或x=-3 …………………………………14′
k<-1时,f(x)min=-k2,此时x=-3 …………………………………15′
-1<k<0时,f(x)min=-1,此时x=1 …………………………………16′

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,且对任意
,且对任意 ,有
,有 .
. ;
; 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数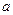 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
) 为实常数).
为实常数). 时,求函数
时,求函数 在
在 上的最小值;
上的最小值; 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
 )
) :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值. 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 。
。 及
及 的值;
的值; 上的解析式;
上的解析式; 的方程
的方程 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围。
的取值范围。