题目内容
已知函数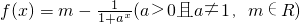 是奇函数.
是奇函数.
(1)求m的值.
(2)当a=2时,解不等式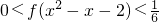 .
.
解:(1)由题意,函数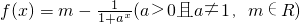 是奇函数.
是奇函数.
∴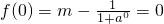 ,解得
,解得
(2)由于a=2,结合(1)可得 =
=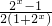
令0<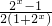 <
< ,即1<2x<4,解得0<x<2
,即1<2x<4,解得0<x<2
再令0<x2-x-2<2,解得x∈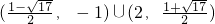
故不等式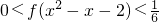 的解集是
的解集是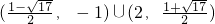
分析:(1)由于函数是定义在R上的奇函数,故可得出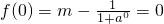 ,由此方程解出参数m的值.
,由此方程解出参数m的值.
(2)此不等式是一个复合型的不等式,直接求解较难可先解出外层函数对应的不等式的解集,再求内层函数对应不等式的解集即可得出所求不等式的解集.
点评:本题考查指数函数的性质及函数奇偶性,解题的关键是熟练掌握理解函数的性质,建立方程解出相应参数,利用函数的单调性解不等式是函数单调性的一个重要运用,本题中所给的不等式是一个复合型的不等式,直接求解较困难,故本题采取了分步求解的策略,解题中注意借鉴.
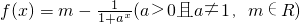 是奇函数.
是奇函数.∴
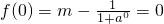 ,解得
,解得
(2)由于a=2,结合(1)可得
 =
=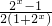
令0<
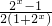 <
< ,即1<2x<4,解得0<x<2
,即1<2x<4,解得0<x<2再令0<x2-x-2<2,解得x∈
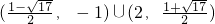
故不等式
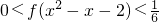 的解集是
的解集是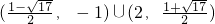
分析:(1)由于函数是定义在R上的奇函数,故可得出
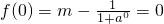 ,由此方程解出参数m的值.
,由此方程解出参数m的值.(2)此不等式是一个复合型的不等式,直接求解较难可先解出外层函数对应的不等式的解集,再求内层函数对应不等式的解集即可得出所求不等式的解集.
点评:本题考查指数函数的性质及函数奇偶性,解题的关键是熟练掌握理解函数的性质,建立方程解出相应参数,利用函数的单调性解不等式是函数单调性的一个重要运用,本题中所给的不等式是一个复合型的不等式,直接求解较困难,故本题采取了分步求解的策略,解题中注意借鉴.

练习册系列答案
相关题目
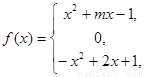
 是奇函数.
是奇函数.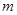 的值;
的值; 在区间
在区间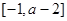 上单调递增,求实数
上单调递增,求实数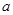 的取值范围;
的取值范围;
 是奇函数.
是奇函数.