题目内容
已知函数f(x)的图象由函数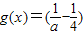 •
•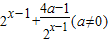 向左平移1个单位得到.
向左平移1个单位得到.(1)求函数f(x)的表达式;
(2)当a=1时,求函数f(x)的最小值;
(3)若函数f(x)的最小值是m,且m>
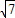 ,求实数a的取值范围.
,求实数a的取值范围.
【答案】分析:(1)根据函数平移的性质进行求解;
(2)把a=1代入f(x),再根据均值不等式进行求解;
(3)对f(x)进行求导,利用导数研究函数的极值,对a进行讨论,研究函数的单调区间,从而进行求解;
解答:解:(1)∵已知函数f(x)的图象由函数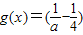 •
•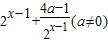 向左平移1个单位得到
向左平移1个单位得到
依题意:f(x)=(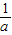 -
- )•2x+
)•2x+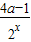
(2)当a=1时,f(x)= •2x+
•2x+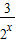 ≥2•
≥2•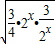 =3;
=3;
(3)∵f′(x)=(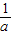 -
- )•2x•ln2+
)•2x•ln2+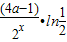
=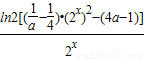 ,
,
∴由f′(x)>0,得:(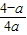 )•(2x)2>4a-1 ①
)•(2x)2>4a-1 ①
①当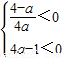 ,即a<0,时,(2x)2>
,即a<0,时,(2x)2>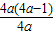 ,
,
当x<log2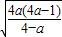 时,函数f(x)递增,
时,函数f(x)递增,
当x>log2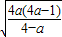 时,函数f(x)递减,
时,函数f(x)递减,
∴函数f(x)只有最大值,矛盾;
②当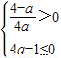 ,即0<a≤
,即0<a≤ 时,①式的解集为R,此时函数f(x)单调递增,
时,①式的解集为R,此时函数f(x)单调递增,
不存在最小值;
③当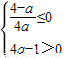 ,即a≥4时,①式的解集为∅.
,即a≥4时,①式的解集为∅.
此时函数f(x)单调递减,不存在最小值;
④当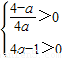 ,即
,即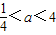 时,(2x)2>
时,(2x)2>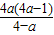 ,
,
∴当x>log2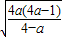 时,函数f(x)递增,
时,函数f(x)递增,
当x<log2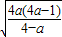 时,函数f(x)递减,
时,函数f(x)递减,
∴函数f(x)当=log2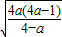 时,有最小值2
时,有最小值2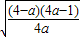 ,
,
∴2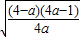 >
>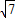 ,
,
∴ <a<2,
<a<2,
综上所述,满足题意设条件的实数a的取值范围是( ,2).
,2).
点评:本题考查了函数的单调性,函数的单调性就是随着x的变大,y在变大就是增函数,y变小就是减函数,利用导数研究函数的单调性,难度比较大;
(2)把a=1代入f(x),再根据均值不等式进行求解;
(3)对f(x)进行求导,利用导数研究函数的极值,对a进行讨论,研究函数的单调区间,从而进行求解;
解答:解:(1)∵已知函数f(x)的图象由函数
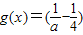 •
•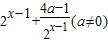 向左平移1个单位得到
向左平移1个单位得到依题意:f(x)=(
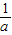 -
- )•2x+
)•2x+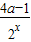
(2)当a=1时,f(x)=
 •2x+
•2x+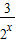 ≥2•
≥2•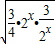 =3;
=3;(3)∵f′(x)=(
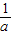 -
- )•2x•ln2+
)•2x•ln2+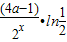
=
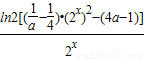 ,
,∴由f′(x)>0,得:(
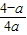 )•(2x)2>4a-1 ①
)•(2x)2>4a-1 ①①当
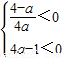 ,即a<0,时,(2x)2>
,即a<0,时,(2x)2>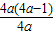 ,
,当x<log2
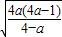 时,函数f(x)递增,
时,函数f(x)递增,当x>log2
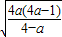 时,函数f(x)递减,
时,函数f(x)递减,∴函数f(x)只有最大值,矛盾;
②当
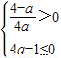 ,即0<a≤
,即0<a≤ 时,①式的解集为R,此时函数f(x)单调递增,
时,①式的解集为R,此时函数f(x)单调递增,不存在最小值;
③当
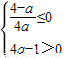 ,即a≥4时,①式的解集为∅.
,即a≥4时,①式的解集为∅.此时函数f(x)单调递减,不存在最小值;
④当
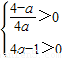 ,即
,即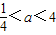 时,(2x)2>
时,(2x)2>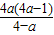 ,
,∴当x>log2
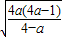 时,函数f(x)递增,
时,函数f(x)递增,当x<log2
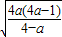 时,函数f(x)递减,
时,函数f(x)递减,∴函数f(x)当=log2
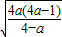 时,有最小值2
时,有最小值2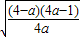 ,
,∴2
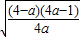 >
>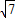 ,
,∴
 <a<2,
<a<2,综上所述,满足题意设条件的实数a的取值范围是(
 ,2).
,2).点评:本题考查了函数的单调性,函数的单调性就是随着x的变大,y在变大就是增函数,y变小就是减函数,利用导数研究函数的单调性,难度比较大;

练习册系列答案
相关题目
已知函数f(x)的图象关于直线x=2对称,且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4,则下列表示大小关系的式子正确的是( )
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(