题目内容
设F1,F2分别为椭圆C:
+
=1(a>b>0)的左、右两个焦点,若椭圆C上的点A(1,
)到F1,F2两点的距离之和等于4.
(1)求出椭圆C的方程和焦点坐标;
(2)过点P(0,
)的直线与椭圆交于两点M、N,若OM⊥ON,求直线MN的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
(1)求出椭圆C的方程和焦点坐标;
(2)过点P(0,
| 3 |
| 2 |
分析:(1)利用椭圆上的点A到F1、F2两点的距离之和是4,可求a,利用点A(1,
)在椭圆上,可求b,从而求出椭圆C的方程和焦点坐标;
(2)设直线MN方程为y=kx+
,代入椭圆C的方程,利用韦达定理即向量知识,建立方程,即可求得直线MN的方程.
| 3 |
| 2 |
(2)设直线MN方程为y=kx+
| 3 |
| 2 |
解答:解:(1)椭圆C的焦点在x轴上,
由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2,
又点A(1,
)在椭圆上,∴
+
=1,∴b2=3,∴c2=1,
所以椭圆C的方程为
+
=1,F1(-1,0),F2(1,0).…(6分)
(2)直线MN不与x轴垂直,设直线MN方程为y=kx+
,
代入椭圆C的方程得(3+4k2)x2+12kx-3=0,
设M(x1,y1),N(x2,y2),则x1+x2=-
,x1x2=-
,且△>0成立.
又
=x1x2+y1y2=x1x2+( kx1+
)(kx2+
)=-
-
+
=0,
∴16k2=5,k=±
,
∴MN方程为y=±
x+
…(14分)
由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2,
又点A(1,
| 3 |
| 2 |
| 1 |
| 22 |
(
| ||
| b2 |
所以椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)直线MN不与x轴垂直,设直线MN方程为y=kx+
| 3 |
| 2 |
代入椭圆C的方程得(3+4k2)x2+12kx-3=0,
设M(x1,y1),N(x2,y2),则x1+x2=-
| 12k |
| 3+4k2 |
| 3 |
| 3+4k2 |
又
| OM |
| •ON |
| 3 |
| 2 |
| 3 |
| 2 |
| 3(1+k2) |
| 3+4k2 |
| 18k2 |
| 3+4k2 |
| 9 |
| 4 |
∴16k2=5,k=±
| ||
| 4 |
∴MN方程为y=±
| ||
| 4 |
| 3 |
| 2 |
点评:本题考查解析几何的基本思想方法,要求学生能正确分析问题,寻找较好的解题方向,同时兼顾考查算理和逻辑的能力,数形结合能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点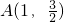 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.