题目内容

当0≤x≤1时， $数学公式$ 恒成立，则a的取值范围是________．

$\text{[math]}$
分析：先去掉绝对值符号，转化为两个不等式，构成不等式组，由于要求参数a的取值范围，可以分离参数a，通过条件0≤x≤1，利用导数求最值的方法求得a的取值范围．
解答：由 $\text{[math]}$ $\text{[math]}$ ，
∴ $\text{[math]}$ ，
当x=0时，a∈R，当x≠0时，有 $\text{[math]}$ $\text{[math]}$ ，
$\text{[math]}$ ，当0＜x≤1可得f′（x）＞0，
∴f（x）在（0，1】是增函数，所以f（x）的最大值为f（1）= $\text{[math]}$ ，
同理可以求得g（x）在（0，1】是减函数，g（x）的最小值为g（1）= $\text{[math]}$ ；
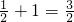∴ $\text{[math]}$ 即 $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题考查绝对值不等式的应用，解题的关键是去掉绝对值符号，转化为不等式组，用分离参数后用求导法求最值，即可求得答案．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

已知点（1，

）是函数f（x）=a^x（a＞0且a≠1）的图象上一点，等比数列{a_n}的前n项和为f（n）-c，数列{b_n}（b_n＞0）的首项为c，且前n项和S_n满足S_n-S_n-1=

（n≥2）．记数列{

}前n项和为T_n，
（1）求数列{a_n}和{b_n}的通项公式；
（2）若对任意正整数n，当m∈[-1，1]时，不等式t²-2mt+

＞T_n恒成立，求实数t的取值范围
（3）是否存在正整数m，n，且1＜m＜n，使得T₁，T_m，T_n成等比数列？若存在，求出m，n的值，若不存在，说明理由．

已知函数f（x）=e^x+ax-1（e为自然对数的底数）．
（I）当a=1时，求过点（1，f（1））处的切线与坐标轴围成的三角形的面积；
（II）若f（x）≥x²在（0，1 ）上恒成立，求实数a的取值范围．

已知函数f（x）=e^x-a（x-1），x∈R，其中a为实数．
（1）若实数a＞0，求函数f（x）在（0，+∞）上的极值．
（2）记函数g（x）f（2x），设函数y=g（x）的图象C与y轴交于P点，曲线C在P点处的切线与两坐标轴所围成的图形的面积为S（a），当a＞1时，求S（a）的最小值；
（3）当x∈（0，+∞）时，不等式f（x）+f′（x）+x³-2x²≥0恒成立，求实数a的取值范围．

已知定义在[1，+∞）上的函数f(x)=

4-|8x-12|(1≤x≤2)

，则（　　）

A．在[1，6）上，方程f（x）-

x=0有5个零点

B．关于x的方程f（x）-

=0（n∈N^*）有2n+4个不同的零点

C．当x∈[2^n-1，2ⁿ]（n∈N^*）时，函数f（x）的图象与x轴围成的面积为4

D．对于实数x∈[1，+∞），不等式xf（x）≤6恒成立

已知函数f（x）=e^x-a（x-1），x∈R，其中a为实数．
（1）若实数a＞0，求函数f（x）在（0，+∞）上的极值．
（2）记函数g（x）f（2x），设函数y=g（x）的图象C与y轴交于P点，曲线C在P点处的切线与两坐标轴所围成的图形的面积为S（a），当a＞1时，求S（a）的最小值；
（3）当x∈（0，+∞）时，不等式f（x）+f′（x）+x³-2x²≥0恒成立，求实数a的取值范围．