题目内容
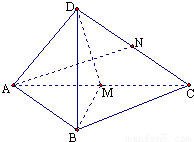
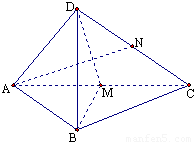
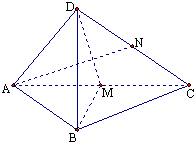 四面体D-ABC,中,AB=BC,在侧面DAC中,中线AN⊥中线DM,且DB⊥AN.
四面体D-ABC,中,AB=BC,在侧面DAC中,中线AN⊥中线DM,且DB⊥AN.(1)求证:平面ACD⊥平面ABC;
(2)若AN=4,DM=3,BD=5,求四面体D-ABC的体积.
分析:(1)根据线面垂直的判定定理,得AN⊥平面BDM,所以AN⊥BM.而等腰△ABC中AC⊥BM,所以BM⊥平面ACD,最后根据面面垂直判定定理,得平面ABC⊥平面ACD;
(2)根据四边形ADNM中,对角线AN、DM互相垂直,得出SADNM=
S△CAD=6,得S△CAD=8.用勾股定理算出BM的长,最后根据BM⊥平面ACD,结合锥体体积公式,可算出四面体D-ABC的体积.
(2)根据四边形ADNM中,对角线AN、DM互相垂直,得出SADNM=
| 3 |
| 4 |
解答:解:(1)∵AN⊥DM,AN⊥DB且DB∩DM=D,
∴AN⊥平面BDM,
∵BM?平面BDM,∴AN⊥BM
又∵△ABC中,AB=BC且M为AC中点,∴AC⊥BM
∵AN、AC是平面ACN内的相交直线,∴BM⊥平面ACD,
∵BM?平面ABC,∴平面ABC⊥平面ACD
(2)连接MN,
∵四边形ADNM中,对角线AN、DM互相垂直,AN=4,DM=3,
∴四边形ADNM面积S=
AN×DM=6
∵MN是△ACD的中位线,
∴△CMN∽△CAD,得S△CMN=
S△CAD,
因此四边形ADNM面积等于
S△CAD=6,得S△CAD=8
∵BM⊥平面ACD,得DM⊥BM
∴Rt△BDM中,BM=
=4
所以四面体D-ABC的体积V=VB-ACD=
S△CAD×BM=
.

∴AN⊥平面BDM,
∵BM?平面BDM,∴AN⊥BM
又∵△ABC中,AB=BC且M为AC中点,∴AC⊥BM
∵AN、AC是平面ACN内的相交直线,∴BM⊥平面ACD,
∵BM?平面ABC,∴平面ABC⊥平面ACD
(2)连接MN,
∵四边形ADNM中,对角线AN、DM互相垂直,AN=4,DM=3,
∴四边形ADNM面积S=
| 1 |
| 2 |
∵MN是△ACD的中位线,
∴△CMN∽△CAD,得S△CMN=
| 1 |
| 4 |
因此四边形ADNM面积等于
| 3 |
| 4 |
∵BM⊥平面ACD,得DM⊥BM
∴Rt△BDM中,BM=
| BD2 -DM2 |
所以四面体D-ABC的体积V=VB-ACD=
| 1 |
| 3 |
| 32 |
| 3 |
点评:本题给出特殊四面体,求证面面垂直并求锥体体积,着重考查了线面垂直、面面垂直的判定与性质和面积体积公式等知识,属于中档题.

练习册系列答案
相关题目
 如图在四面体D-ABC中,OA、0B、OC两两垂直,且OB=OC=3,OA=4.给出以下判断:
如图在四面体D-ABC中,OA、0B、OC两两垂直,且OB=OC=3,OA=4.给出以下判断: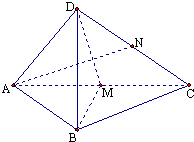 四面体D-ABC,中,AB=BC,在侧面DAC中,中线AN⊥中线DM,且DB⊥AN.
四面体D-ABC,中,AB=BC,在侧面DAC中,中线AN⊥中线DM,且DB⊥AN.