题目内容
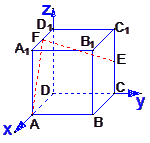
棱长为2的正方体A1B1C1D1-ABCD中，E、F分别是C1C和D1A1的中点，
（1）求异面直线
与
所成的角的余弦值；
（2）求点A到EF的距离．
（1）异面直线
与
所成的角的余弦值为
；（2）A到EF的距离为
．
解析:
（1）如图，以D为原点，DA、DC、DD1分别为x轴、
y轴、z轴建立空间直角坐标系，则由已知得
A（2，0，0），B（2，2，0），E（0，2，1），F（1，0，2）；
∴
=（0，2，0），
=（1，
，1），
=（1，0，），
∴ ||=2，||=
，
=
；
= 
, 
=
，
∴
与
夹角的余弦值为cos
=
=
．
∵异面直线所成角的范围是
，向量的夹角范围是
；
∴异面直线与所成的角的余弦值为．
（2）由（1）得=
，||=；
∴在
方向上的射影为
=
，
∴A到EF的距离为．
练习册系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
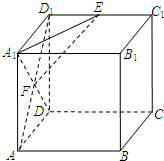（2008•杨浦区二模）在棱长为2的正方体ABCD-A1B1C1D1中，（如图）E是棱C1D1的中点，F是侧面AA1D1D的中心．
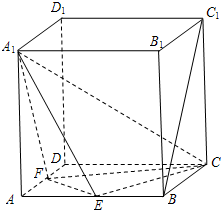（2007•静安区一模）（文）如图，在棱长为2的正方体ABCD-A1B1C1D1中，点E、F分别是棱AB、AD的中点．求：
（文）如图，在棱长为2的正方体ABCD-A1B1C1D1中，点E、F分别是棱AB、AD的中点．求：
