题目内容
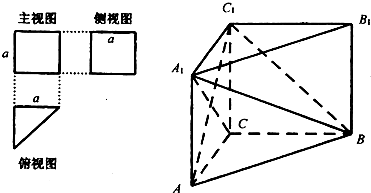
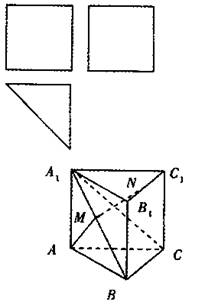
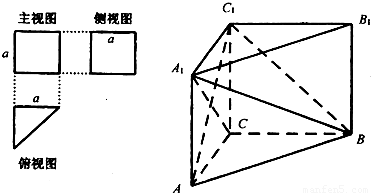
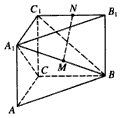
一个多面体的三视图及直观图如图所示,M,N分别是A1B,B1C1的中点.
(Ⅰ)求证:MN⊥平面A1BC;
(Ⅱ)求直线BC1和平面A1BC所成角的大小;
(Ⅲ)求二面角A-A1B-C的大小.
(Ⅰ)求证:MN⊥平面A1BC;
(Ⅱ)求直线BC1和平面A1BC所成角的大小;
(Ⅲ)求二面角A-A1B-C的大小.
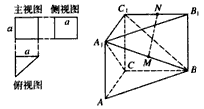
| 解:由三视图可知,在这个多面体的直观图中,AA1⊥平面ABC, 且AC⊥BC,AC=BC=CC1=a, (Ⅰ)连接AC1,AB1,因为BC⊥平面ACC1A1, 所以BC⊥AC1,在正方形ACC1A1中,A1C⊥AC1, 又因为BC∩A1C=C, 所以AC1⊥平面A1BC, 由正方形性质知AB1过A1B的中点M, 在△AB1C1中,MN∥AC1, 所以MN⊥平面A1BC。 |
 |
| (Ⅱ)由题意CA,CB,CC1两两垂直, 故以C为原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴, 建立空间直角坐标系, 又AC=BC=CC1=a,则B(0,a,0),B1(0,a,a),A(a,0,0), 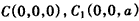 , ,则 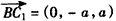 , ,又AC1⊥平面A1BC, 故 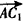 为平面A1BC的法向量, 为平面A1BC的法向量,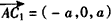 , ,所以, 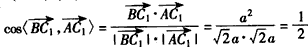 , ,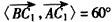 , ,因此直线BC1和平面A1BC所成角的大小为30°。 (Ⅲ)AB中点E的坐标为 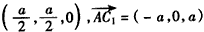 , ,易知 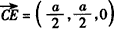 为平面AA1B的法向量,又 为平面AA1B的法向量,又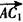 为平面A1BC的法向量, 为平面A1BC的法向量,设二面角A-A1B-C为θ, 则 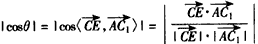 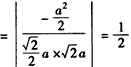 , ,由题意,知θ为锐角,所以θ=60°, 即二面角A-A1B-C为60°。 |

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目