题目内容
f(x)=
,x=0,则f{f[f(-3)]}等于( )
|
分析:应从内到外逐层求解,计算时要充分考虑自变量的范围.根据不同的范围代不同的解析式.
解答:解:由题可知:∵-3<0,∴f(-3)=0,
∴f[f(-3)]=f(0)=π>0,
∴f{f[f(-3)]}=f(π)=π2
故选C
∴f[f(-3)]=f(0)=π>0,
∴f{f[f(-3)]}=f(π)=π2
故选C
点评:本题考查的是分段函数求值问题.在解答的过程当中充分体现了复合函数的思想、问题转化的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
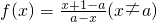
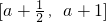 时,求f(x)的值域;
时,求f(x)的值域;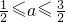 ,求g(x)的最小值.
,求g(x)的最小值.