题目内容

在△ABC中，若∠A= $数学公式$ ，tan（A+B）=7，AC=3 $数学公式$ ，则△ABC的面积为________．

$\text{[math]}$
分析：利用三角形的内角和，求解tanC，通过同角三角函数的基本关系式，求解sinC的值，利用A求解sinB，通过正弦定理求解c，然后求解△ABC的面积．
解答：在△ABC中，∵A+B+C=π，∴tanC=tan[π-（A+B）]=-tan（A+B）
∵tan（A+B）=7，∴tanC=-7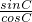，∴ $\text{[math]}$ =-7
∵sin²C+cos²C=1，C∈（0，π），
∴sinC= $\text{[math]}$
∵∠A= $\text{[math]}$ ，tan（A+B）=7，∴ $\text{[math]}$ =7
∴tanB= $\text{[math]}$
∵C∈（0，π），∴sinB= $\text{[math]}$
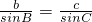∴由正弦定理 $\text{[math]}$ ，代入得到c=7
∴S_△ABC= $\text{[math]}$ bcsinA= $\text{[math]}$ ×3 $\text{[math]}$ ×7×sin $\text{[math]}$ = $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题考查三角形的内角和，同角三角函数的基本关系式的应用，正弦定理的应用，考查计算能力，属于中档题．

练习册系列答案

综合自测系列答案

走进重高培优测试系列答案

中考全程突破系列答案

名师金手指大试卷系列答案

标准课堂测试卷系列答案

智慧翔夺冠金卷系列答案

名校导练系列答案

目标实施手册测试卷系列答案

智慧通自主练习系列答案

第一微卷系列答案

相关题目

给出命题：
①函数y=2sinx-cosx的值域是[-2，1]；
②函数y=sinπxcosπx是周期为2的奇函数；
③x=-

π是函数y=sin(x+

)的一条对称轴；
④若sin2α＜0，cosα-sinα＜0，则α一定为第二象限角；
⑤在△ABC中，若A＞B则sinA＞sinB．
其中正确命题的序号为

在△ABC中，若a=7，b=3，c=8，则其面积等于（　　）

在△ABC中，若∠A=60°，∠B=45°，BC=

下列命题中，真命题的个数为（　　）
（1）在△ABC中，若A＞B，则sinA＞sinB；
（2）已知

=(-2，-1)，则

上的投影为-2；
（3）已知p：?x∈R，cosx=1，q：?x∈R，x²-x+1＞0，则“p∧￢q”为假命题；
（4）已知函数f(x)=sin(ωx+

)-2（ω＞0）的导函数的最大值为3，则函数f（x）的图象关于x=

已知α为锐角，且tanα=

-1，函数f(x)=2xtan2α+sin(2α+

)，数列{a_n}的首项a₁=1，a_n+1=f（a_n）．
（1）求函数f（x）的表达式；
（2）在△ABC中，若∠A=2α，∠C=

，BC=2，求△ABC的面积
（3）求数列{a_n}的前n项和S_n．