Question

判断下列函数的奇偶性.

（1）f（x）=x+；                    （2）f（x）=x²+；

（3）f（x）=；                   （4）f（x）=；

（5）f（x）=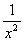

Answer 1

解析：判断函数奇偶性的关键是先看定义域是否关于原点对称，再看f（-x）与f（x）的关系.

解：（1）定义域为A={x|x∈R，且x≠0}.

∵对定义域内的每一个x，都有f（-x）=-x+=-（x+）=-f（x），

∴f（x）=x+为奇函数.

（2）定义域为A={x|x∈R，且x≠0}.

∵对定义域内的每一个x，都有f（-x）=（-x）²+=x²+=f（x），

∴函数f（x）=x²+为偶函数.

（3）函数的定义域为A={x|x＞0}，关于原点不对称，

∴函数f（x）=为非奇非偶函数.

（4）由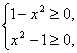得x²=1.∴x=±1.

∴函数的定义域为{-1，1}.于是f（x）=0，x∈{-1，1}，

    满足f（-x）=f（x）=0，f（-x）=-f（x）=0.

∴f（x）既是奇函数，又是偶函数.

（5）分段函数f（x）的定义域为（-∞，0）∪（0，+∞），关于原点对称.

    当x＞0时，-x＜0，f（-x）=-（-x）²-1=-（x²+1）=-f（x）；

    当x＜0时，-x＞0，f（-x）=（-x）²+1=x²+1=-（-x²-1）=-f（x） .

    综上所述，在（-∞，0）∪（0，+∞）上总有f（-x）=-f（x），

∴f（x）是奇函数.