题目内容
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
2sin(3x-
)
| π |
| 4 |
2sin(3x-
)
.| π |
| 4 |
分析:由函数的最大最小值,求出振幅A=2.设函数的周期为T,得
T=
,所以T=
=
,解之得ω=3.最后根据当x=
时函数有最大值为2,代入解析式建立关于φ的等式,解出φ=-
即可得到函数的解析式.
| 3 |
| 4 |
| π |
| 2 |
| 2π |
| ω |
| 2π |
| 3 |
| π |
| 4 |
| π |
| 4 |
解答:解:∵函数的最大最小值分别为2、-2,且A>0,∴A=2.
又∵函数的周期T=[
-(-
)]÷
=
,且ω>0,
∴
=
,解之得ω=3.
可得函数的解析式为f(x)=2sin(3x+φ),
又∵当x=
时,函数有最大值为2,
∴2sin(3•
+φ)=2,得sin(
+φ)=1,可得
+φ=
+2kπ(k∈Z)
∵|φ|<
,得-
<φ<
,∴取k=0得φ=
-
=-
.
即函数的解析式为f(x)=2sin(3x-
),
故答案为:2sin(3x-
)
又∵函数的周期T=[
| π |
| 4 |
| π |
| 4 |
| 3 |
| 4 |
| 2π |
| 3 |
∴
| 2π |
| ω |
| 2π |
| 3 |
可得函数的解析式为f(x)=2sin(3x+φ),
又∵当x=
| π |
| 4 |
∴2sin(3•
| π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| π |
| 2 |
∵|φ|<
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
即函数的解析式为f(x)=2sin(3x-
| π |
| 4 |
故答案为:2sin(3x-
| π |
| 4 |
点评:本题给出正弦型三角函数在一个周期上的图象,求函数的解析式.着重考查了三角函数的图象变换和根据图象确定函数的解析式等知识,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
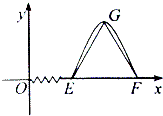 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于 函数f(x)=Asin(ωx+?)(其中A>0,ω>0,
函数f(x)=Asin(ωx+?)(其中A>0,ω>0,