题目内容
已知f(x)是定义在(0,+∞)上的增函数,且f(
解:2=f(2)+f(2),而f(![]() )=f(x)-f(y)可以变形为f(y)+f(
)=f(x)-f(y)可以变形为f(y)+f(![]() )=f(x).
)=f(x).
令y=2,![]() =2,即x=2y=4,
=2,即x=2y=4,
则有f(2)+f(2)=f(4),∴2=f(4).
∴f(x)-f(![]() )≤2可以变形为f[x(x-3)]≤f(4).
)≤2可以变形为f[x(x-3)]≤f(4).
又∵f(x)是定义在(0,+∞)上的增函数,
∴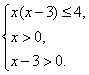 解得3<x≤4.
解得3<x≤4.
∴原不等式的解集为{x|3<x≤4}.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 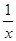 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
