题目内容
已知函数f(x)=ax-ln(-x),x∈[-e,0),其中e是自然常数,a∈R。
(1)若函数f(x)单调递增,求实数a的范围;
(2)是否存在实数a,使f(x)的最小值是3,如果存在,求出a的值;如果不存在,说明理由。
(1)若函数f(x)单调递增,求实数a的范围;
(2)是否存在实数a,使f(x)的最小值是3,如果存在,求出a的值;如果不存在,说明理由。
解:(1)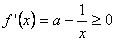 对于
对于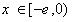 恒成立,即
恒成立,即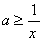 对
对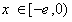 恒成立,
恒成立,
∴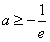 ,
,
即a的取值范围是[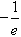 ,+∞)。
,+∞)。
(2)假设存在实数a,使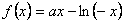 有最小值3,
有最小值3,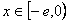
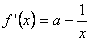 ,
,
①当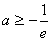 时,由于
时,由于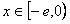 ,则
,则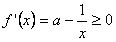 ,
,
∴函数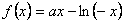 是[-e,0)上的增函数,
是[-e,0)上的增函数,
∴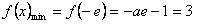 ,解得:
,解得: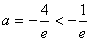 (舍去);
(舍去);
②当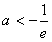 时,则当
时,则当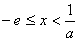 时,
时,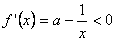 ,此时
,此时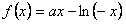 是减函数;
是减函数;
当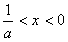 时,
时,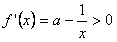 ,此时
,此时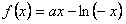 是增函数,
是增函数,
∴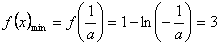 ,
,
解得: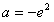 。
。
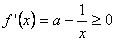 对于
对于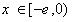 恒成立,即
恒成立,即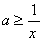 对
对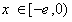 恒成立,
恒成立,∴
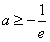 ,
,即a的取值范围是[
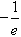 ,+∞)。
,+∞)。(2)假设存在实数a,使
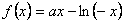 有最小值3,
有最小值3,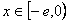
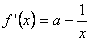 ,
,①当
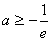 时,由于
时,由于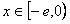 ,则
,则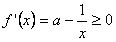 ,
,∴函数
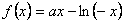 是[-e,0)上的增函数,
是[-e,0)上的增函数,∴
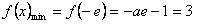 ,解得:
,解得: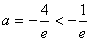 (舍去);
(舍去);②当
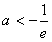 时,则当
时,则当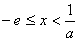 时,
时,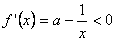 ,此时
,此时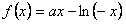 是减函数;
是减函数;当
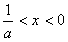 时,
时,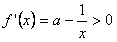 ,此时
,此时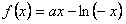 是增函数,
是增函数,∴
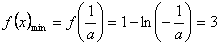 ,
,解得:
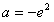 。
。
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目