题目内容

记等差数列{a_n}的前n项的和为S_n，利用倒序求和的方法得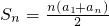： $数学公式$ ；类似地，记等比数列{b_n}的前n项的积为T_n，且 $数学公式$ ，试类比等差数列求和的方法，将T_n表示成首项b₁，末项b_n与项数n的一个关系式，即T_n=________．

$\text{[math]}$
分析：等差数列与等比数列的定义的区别在于差与比，故类比倒序相加求和，可知倒序相乘求积，再利用等比数列的性质，即可得到结论．
解答：由题意，T_n=b₁b₂…b_n①，倒序为T_n=b_nb_n-1…b₁②，
①×②可得 $\text{[math]}$ =（b₁b₂…b_n）（b_nb_n-1…b₁）= $\text{[math]}$
∵ $\text{[math]}$
∴ $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题考查类比推理，解题的关键是类比解题的方法，类比倒序相加求和，可知倒序相乘求积．

练习册系列答案

快乐寒假甘肃少年儿童出版社系列答案

寒假篇假期园地广西师范大学出版社系列答案

快乐寒假吉林教育出版社系列答案

创新成功学习快乐寒假四川大学出版社系列答案

寒假生活河北少年儿童出版社系列答案

寒假作业知识出版社系列答案

拓展阅读寒假能力训练吉林教育出版社系列答案

寒假百分百云南科技出版社系列答案

黄金假期寒假作业武汉大学出版社系列答案

寒假期导航学年知识大归纳辽海出版社系列答案

相关题目

记等差数列{a_n}的前n项和为S_n，若a1=

，S₄=20，则S₆=（　　）

记等差数列{a_n}的前n项和为S_n，设S₃=12，且2a₁，a₂，a₃+1成等比数列，求S_n．

记等差数列{a_n}的前n项和为S_n，若a1=

，S₄=20，则S₆=

（2006•广州一模）记等差数列{a_n}的前n项和为S_n，若a₉=10，则 S₁₇=

（2013•盐城三模）记等差数列{a_n}的前n项和为S_n．
（1）求证：数列{

}是等差数列；
（2）若a₁=1，且对任意正整数n，k（n＞k），都有

成立，求数列{a_n}的通项公式；
（3）记b_n=aan（a＞0），求证：