题目内容
向量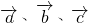
满足
，
，
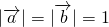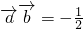，则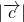
的最大值为________．
2
分析：利用向量的数量积求出
与
的夹角；利用向量的运算法则作出图；结合图，判断出四点共圆；利用正弦定理求出外接圆的直径，求出最大值．
解答：
解：由，，，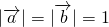
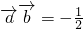可得1×1×cos
=
，∴cos=，∴=120°，
如图所示：设
，
，
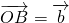，则
，
，
∴
，
=1+1-2（-
）=3，∴
=
，
由三角形的正弦定理得外接圆的直径2R=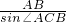
=2，
当OC为直径时，它的模最大，且最大值为2，
故答案为：2
点评：本题考查向量的数量积公式、向量的运算法则、四点共圆的判断、三角形的正弦定理，属于中档题．
分析：利用向量的数量积求出
与的夹角；利用向量的运算法则作出图；结合图，判断出四点共圆；利用正弦定理求出外接圆的直径，求出最大值．解答：
解：由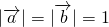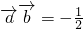，，，可得1×1×cos
=，∴cos=，∴=120°，如图所示：设
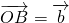，，，则，，∴
，=1+1-2（-）=3，∴=，由三角形的正弦定理得外接圆的直径2R=
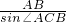=2，当OC为直径时，它的模最大，且最大值为2，
故答案为：2
点评：本题考查向量的数量积公式、向量的运算法则、四点共圆的判断、三角形的正弦定理，属于中档题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
满足
，
，
，则
的最大值是_____________． 
满足
，
，
，则
的最大值是
B.
C.
D.
1
满足|2
|≤3，则
的最小值是 ．
满足|2
|≤3，则
的最小值是 ．
满足
，
，
，则
的最大值为 ．