题目内容
已知向量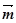 =(sinA,cosA),
=(sinA,cosA), 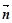 =
=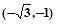 ,
,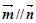 ,且A为锐角.
,且A为锐角.
(1)求角A的大小;
(2)求函数f(x)=cos2x+4cosAsinx,(xÎR) 最大值及取最大值时x的集合.
(1) A=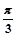 ;(2) f(x)有最大值
;(2) f(x)有最大值 ,x=2kp+
,x=2kp+ 或x=2kp+
或x=2kp+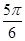 (kÎZ)
(kÎZ)
解析试题分析:(1)∵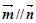 ∴-sinA+
∴-sinA+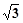 cosA=0 3分
cosA=0 3分
∴tanA=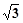 ,A为锐角,∴A=
,A为锐角,∴A=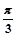 6分
6分
(2)由(1)知cosA=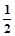
所以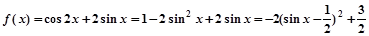 8分
8分
因为x∈R,所以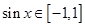 ,因此,当
,因此,当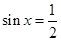 时,f(x)有最大值
时,f(x)有最大值 10分
10分
且x=2kp+ 或x=2kp+
或x=2kp+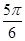 (kÎZ) 12分
(kÎZ) 12分
考点:本题主要考查平面向量的平行,平面向量的坐标运算,三角函数的和差倍半公式,三角函数、二次函数的图象和性质。
点评:中档题,本题综合考查平面向量的平行,平面向量的坐标运算,三角函数的和差倍半公式,三角函数、二次函数的图象和性质。向量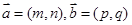 平行,等价于
平行,等价于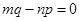 。利用向量的运算,得到三角函数式,运用三角公式进行化简,以便于利用其它知识解题,是这类题的显著特点。
。利用向量的运算,得到三角函数式,运用三角公式进行化简,以便于利用其它知识解题,是这类题的显著特点。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
菱形ABCD边长为2,∠BAD=120°,点E,F分别别在BCCD, ,若
,若 ,则
,则
A. | B. | C. | D.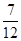 |
 为原点,
为原点, .
. 的坐标及
的坐标及 ;
; ,求
,求 及
及 的坐标;
的坐标; .
. ,
,  ,
,  的值。
的值。 为何值时,
为何值时, 与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向? ,且
,且 .
. 和
和 ; (2)求
; (2)求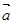 方向上的投影; (3)求
方向上的投影; (3)求 和
和 ,使
,使 .
.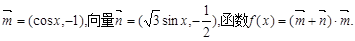
 的最小正周期T;
的最小正周期T; ,b,c分别为△ABC内角A,B,C的对边,A为锐角,
,b,c分别为△ABC内角A,B,C的对边,A为锐角,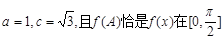 上的最大值,求A,b和△ABC的面积.
上的最大值,求A,b和△ABC的面积. 与
与  共线,设函数
共线,设函数  .
.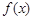 的周期及最大值;
的周期及最大值; ,边 BC=
,边 BC= ,
, ,求 △ABC 的面积.
,求 △ABC 的面积. 
 =
=