题目内容
函数y=ln(
)的图象大致是( )
| x-sinx |
| x+sinx |
A、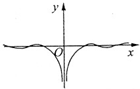 |
B、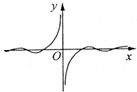 |
C、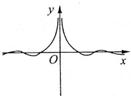 |
D、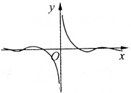 |
分析:由函数的解析式可得函数的定义域关于原点对称,根据f(-x)=f(x),可得函数的图象关于y轴对称,故排除B、D,再根据当x∈(0,1)时,ln(
)<0,从而排除C,从而得到答案.
| x-sinx |
| x+sinx |
解答:解:∵函数y=ln(
),∴x+sinx≠0,x≠0,故函数的定义域为{x|x≠0}.
再根据y=f(x)的解析式可得f(-x)=ln(
)=ln(
)=f(x),
故函数f(x)为偶函数,故函数的图象关于y轴对称,故排除B、D.
当x∈(0,1)时,∵0<sinx<x<1,∴0<
<1,
∴函数y=ln(
)<0,故排除C,只有A满足条件,
故选:A.
| x-sinx |
| x+sinx |
再根据y=f(x)的解析式可得f(-x)=ln(
| -x+sinx |
| -x-sinx |
| x-sinx |
| x+sinx |
故函数f(x)为偶函数,故函数的图象关于y轴对称,故排除B、D.
当x∈(0,1)时,∵0<sinx<x<1,∴0<
| x-sinx |
| x+sinx |
∴函数y=ln(
| x-sinx |
| x+sinx |
故选:A.
点评:本题主要考查正弦函数的图象特征,函数的奇偶性的判断,属于中档题.

练习册系列答案
相关题目
若函数y=f(x)图象上的任意一点P的坐标(x,y)满足条件|x|≥|y|,则称函数f(x)具有性质S,那么下列函数中具有性质S的是( )
| A、f(x)=ex-1 | B、f(x)=ln(x+1) | C、f(x)=sinx | D、f(x)=tanx |
