题目内容
计算下列几个式子,
①tan25°+tan35°+
tan25°tan35°,
②2(sin35°cos25°+sin55°cos65°),
③
,
④
,
结果为
的是( )
①tan25°+tan35°+
| 3 |
②2(sin35°cos25°+sin55°cos65°),
③
| 1+tan15° |
| 1-tan15° |
④
tan
| ||
1-tan2
|
结果为
| 3 |
| A.①② | B.③ | C.①②③ | D.②③④ |
∵tan60°=tan(25°+35°)=
=
∴tan25°+tan35°=
(1-tan25°tan35°)
∴tan25°+tan35°+
tan25°tan35°=
,①符合
2(sin35°cos25°+sin55°cos65°)=2(sin35°cos25°+cos35°sin25°)=2sin60°=
,②符合
=tan(45°+15°)=tan60°=
,③符合
=
=
tan
=
,④不符合
故结果为
的是①②③
故选C
| tan25°+tan35° |
| 1-tan25°tan35° |
| 3 |
∴tan25°+tan35°=
| 3 |
∴tan25°+tan35°+
| 3 |
| 3 |
2(sin35°cos25°+sin55°cos65°)=2(sin35°cos25°+cos35°sin25°)=2sin60°=
| 3 |
| 1+tan15° |
| 1-tan15° |
| 3 |
tan
| ||
1-tan2
|
| 1 |
| 2 |
2tan
| ||
1-tan2
|
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
故结果为
| 3 |
故选C

练习册系列答案
相关题目
 ,
, ,
,  ,
,
 的是 (填上所有你认为正确答案的序号)
的是 (填上所有你认为正确答案的序号) ,
, ,
,  ,
,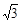 的是(
)
的是(
)