题目内容
以D
为圆心，1为半径的圆的极坐标方程为________．
ρ2+1-2
分析：求出圆心的直角坐标，求得圆的方程为 x2+y2-2x-2y+1=0，化为极坐标方程为 ρ2-2ρcosθ-2ρsinθ+1=0，化简可得结果．
解答：圆心D 的直角坐标为（1，1），半径等于1，故圆的方程为 （x-1）2+（y-1）2=1，
即 x2+y2-2x-2y+1=0，化为极坐标方程为 ρ2-2ρcosθ-2ρsinθ+1=0，
即 ρ2+1-2
，
故答案为：ρ2+1-2．
点评：本题考查求圆的极坐标方程的方法，求出圆的直角坐标方程，是解题的关键．
分析：求出圆心的直角坐标，求得圆的方程为 x2+y2-2x-2y+1=0，化为极坐标方程为 ρ2-2ρcosθ-2ρsinθ+1=0，化简可得结果．
解答：圆心D
的直角坐标为（1，1），半径等于1，故圆的方程为 （x-1）2+（y-1）2=1，即 x2+y2-2x-2y+1=0，化为极坐标方程为 ρ2-2ρcosθ-2ρsinθ+1=0，
即 ρ2+1-2
，故答案为：ρ2+1-2
．点评：本题考查求圆的极坐标方程的方法，求出圆的直角坐标方程，是解题的关键．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
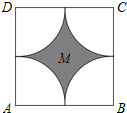如图，在边长为2的正方形ABCD内随机取一点P，分别以A、B、C、D为圆心、1为半径作圆，在正方形ABCD内的四段圆弧所围成的封闭区域记为M（阴影部分），则点P取自区域M的概率是（ ）
（2012•顺河区一模）选做题：几何证明选讲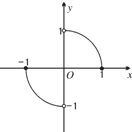
函数y=f（x）的图象是以原点为圆心，1为半径的两段圆弧，则不等式f（x）＞f（-x）+x的解集为（ ）
为圆心，1为半径的圆的极坐标方程为 ．