题目内容
已知各项均为正数的数列{an}的前n项的和为Sn,且对任意的n∈N*,都有2Sn=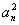 +an
+an
(1)求数列{an}的通项公式;
(2)数列{bn}满足b1=1,2bn+1-bn=0,(n∈N*).若cn=anbn,求数列{cn}的前n项和Tn
解:(1)当n=1时,由2a1=2S1= ,a1>0,得a1=1
,a1>0,得a1=1
当n≥2时,由2an=2Sn-2Sn-1=(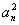 +an)-(
+an)-( )
)
得(an+an-1)(an-an-1-1)=0
因为an+an-1>0,所以an-an-1=1
故an=1+(n-1)×1=n
(2)由b1=1, ,得bn=
,得bn= ,则cn=n
,则cn=n
因为 Tn= ,
,
所以 
得 
=2-(n+2)
所以 Tn=4-(n+2)

练习册系列答案
相关题目
已知双曲线 的渐近线方程为
的渐近线方程为 ,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )
,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )
| A. | B. | C. | D.1 |
 (其中A>0,
(其中A>0, )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,则只需将g(x)=sin2x的图象( )
的图象,则只需将g(x)=sin2x的图象( )
 个长度单位 B. 向左平移
个长度单位 B. 向左平移 个长度单位 D. 向左平移
个长度单位 D. 向左平移 .
. 时,求
时,求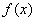 的单调区间;
的单调区间; 有解,求实数m的取值菹围;
有解,求实数m的取值菹围; .
.


 过圆C:
过圆C: 的圆心C,且与直线OC垂直,则直线
的圆心C,且与直线OC垂直,则直线 成立的( )
成立的( ) 表示的平面区域为D,若函数
表示的平面区域为D,若函数 的图像上存在区域D上的点,则实数
的图像上存在区域D上的点,则实数 的取值范围是( )
的取值范围是( ) (B)
(B)
 (D)
(D)
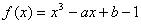 是定义在
是定义在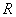 上的奇函数,且在
上的奇函数,且在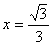 时取最得极值,则
时取最得极值,则 的值为( )A、
的值为( )A、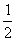 B、
B、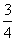 C、1 D、2
C、1 D、2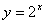 图象上存在点(x,y)满足约束条件
图象上存在点(x,y)满足约束条件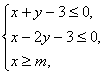 则实数m的最大值为
则实数m的最大值为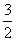 C.1 D.
C.1 D.