题目内容
已知圆方程 .
.
(1)若圆与直线 相交于M,N两点,且
相交于M,N两点,且 (
( 为坐标原点)求
为坐标原点)求 的值;
的值;
(2)在(1)的条件下,求以 为直径的圆的方程.
为直径的圆的方程.
(1)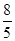 ;(2)
;(2)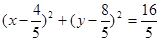 .
.
解析试题分析:首先确定方程 表示圆时
表示圆时 应满足的条件;
应满足的条件;
设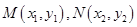 ,
, 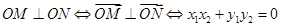 ,
,
利用韦达定理,建设立关于 的方程,解方程可得
的方程,解方程可得 的值.
的值.
在(1)的条件下,以 为直径的圆过原点,利用韦达定理求出
为直径的圆过原点,利用韦达定理求出 的中点
的中点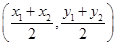 ,从而也就易于求出半径,得到圆的方程.
,从而也就易于求出半径,得到圆的方程.
试题解析:解:(1)由 得:
得:
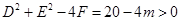
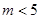 2分
2分
于是由题意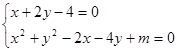
把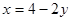 代入
代入
得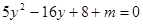 3分
3分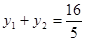 ,
,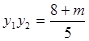 4分
4分
∵ 得出:
得出: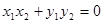 5分
5分
∴
∴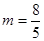 8分
8分
(2)设圆心为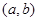
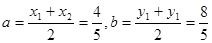 .9分
.9分
半径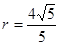 12分
12分
圆的方程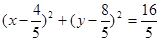 13分
13分
考点:1、圆的方程;2、直线与圆的位置关系;3、韦达定理的应用;4、向量垂直的条件.

练习册系列答案
相关题目
 经过点
经过点 和
和
 上,求圆
上,求圆 的圆心在直线
的圆心在直线 上,且与
上,且与 轴交于两点
轴交于两点 ,
, .
.
 的圆
的圆 的三个顶点
的三个顶点 ,
,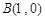 ,
,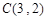 ,其外接圆为
,其外接圆为 .
. 过点
过点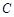 ,且被
,且被 上的任意一点
上的任意一点 ,若在以
,若在以 ,使得点
,使得点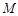 是线段
是线段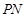 的中点,求
的中点,求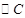 的半径
的半径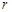 的取值范围.
的取值范围.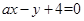 与圆
与圆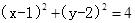 。
。 ,求a的值。
,求a的值。 直线
直线
 取何实数,直线
取何实数,直线 与圆C恒相交;
与圆C恒相交;