Question

在△ABC中，∠ABC=45°，∠ACB=60°，△ABC绕BC旋转一周，记以AB为母线的圆锥为M₁，记以AC为母线的圆锥为M₂，m是圆锥M₁任一母线，则圆锥M₂的母线中与m垂直的直线有

2

条．

Answer 1

分析：以圆锥底面圆心O为原点，建立空间直角坐标系，设圆锥M₁母线为BA，圆锥M₂的母线为CP，其中P（x，y，0），则有

AB

•

CP

=0，通过方程解的个数确定直线条数．

解答：解：作AO⊥BC于O，设不妨设m=AB，以O为原点，建立空间直角坐标系．


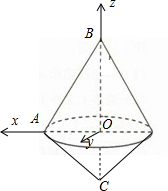
设AB=1，，∠ABC=45°，则AO=BO=

2

2

，又∠ACB=60°∴OC=

6

6

，∴A（

2

2

，0，0），B（0，0，

2

2

）C（0，0，-

6

6

）  P（x，y，0），

AB

=（-

2

2

，0，

2

2

），

CP

=（x，y，

6

6

）
若母线AB⊥CP，则

AB

•

CP

=0∴-

2

2

x+

2

2

×

6

6

=0，解得x=

6

6

，又P在以O为圆心的圆周上，∴x²+y²=

1

2

，解得y=±

3

3

，
P有两个位置使母线AB⊥CP，即圆锥M₂的母线中与m垂直的直线有 两条．
故答案为：2

点评：本题考查直线垂直的判定，利用向量数量积运算，降低了思维难度，使问题容易获解．