题目内容
已知函数f（x）=
sin2x+2cos2x+m在区间[0，
]上的最大值为6
（1）求常数m的值及函数f（x）图象的对称中心；
（2）作函数f（x）关于y轴的对称图象得函数f1（x）的图象，再把函数f1（x）的图象向右平移
个单位得函数f2（x）的图象，求函数f2（x）的单调递减区间．
sin2x+2cos2x+m在区间[0，]上的最大值为6（1）求常数m的值及函数f（x）图象的对称中心；
（2）作函数f（x）关于y轴的对称图象得函数f1（x）的图象，再把函数f1（x）的图象向右平移
个单位得函数f2（x）的图象，求函数f2（x）的单调递减区间．解：（1）函数f（x）=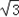
sin2x+2cos2x+m=
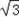sin2x+cos2x+1+m=2sin（2x+
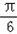）+1+m，
函数f（x）=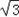
sin2x+2cos2x+m在区间[0，
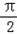]上的最大值为6，
所以m=3，
函数的表达式为f（x）=2sin（2x+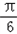
）+4；它的对称中心为（
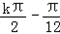，0），k∈Z．
（2）函数f（x）关于y轴的对称图象得函数f1（x）=2sin（﹣2x+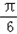
）+4的图象，
函数f1（x）的图象向右平移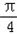
个单位得函数
f2（x）=2sin（﹣2x+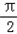
+
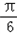）+4=2cos（2x﹣
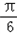）+4的图象；
函数f2（x）的单调递减区间为：2kπ≤2x﹣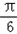
≤2kπ+π，kπ
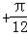≤x≤kπ+
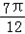k∈Z．
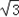sin2x+2cos2x+m=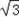sin2x+cos2x+1+m=2sin（2x+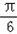）+1+m，函数f（x）=
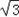sin2x+2cos2x+m在区间[0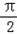，]上的最大值为6，所以m=3，
函数的表达式为f（x）=2sin（2x+
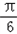）+4；它的对称中心为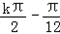（，0），k∈Z．（2）函数f（x）关于y轴的对称图象得函数f1（x）=2sin（﹣2x+
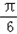）+4的图象，函数f1（x）的图象向右平移
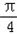个单位得函数f2（x）=2sin（﹣2x+
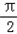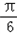+）+4=2cos（2x﹣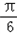）+4的图象；函数f2（x）的单调递减区间为：2kπ≤2x﹣
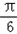≤2kπ+π，kπ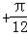≤x≤kπ+ 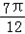k∈Z．
练习册系列答案
相关题目
