题目内容
过直线
上的动点
作抛物线
的两切线
,
为切点.
（1）若切线的斜率分别为
，求证：
为定值.
（2）求证：直线
过定点．
（本小题满分10分）
解：（1）设过
作抛物线
的切线的斜率为
，则切线的方程为
，
与方程联立，消去
，得
.
因为直线与抛物线相切，所以
，
即
. 由题意知，此方程两根为
，
∴
(定值). ……………………………5分
（2）设
，由，得
.
所以在
点处的切线斜率为：
，因此，切线方程为：
.
由
，化简可得，
.
同理，得在点
处的切线方程为
.
因为两切线的交点为
，故
,
.
∴
两点在直线
上，即直线
的方程为：.
当
时,
，所以直线经过定点
. …………………………10分
练习册系列答案
阳光课堂课时作业系列答案
相关题目
)为方向向量的直线l过点(0，
)，抛物线C：y2＝2px(p＞0)的顶点关于直线l的对称点在该抛物的准线上．
(O为原点，A、B异于原点)，试求点N的轨迹方程．
)为方向向量的直线l过点(0, 
(p>0)的顶点关于直线l的对称点在该抛物的准线上．
(O为原点，A、B异于原点)，试求点N的轨迹方程．
)为方向向量的直线l过点(0, 
)，抛物线C： 
(p>0)的顶点关于直线l的对称点在该抛物的准线上．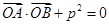
(O为原点，A、B异于原点)，试求点N的轨迹方程．