题目内容
定义在 上的函数
上的函数 的图像关于
的图像关于 对称,且当
对称,且当 时,
时, (其中
(其中 是
是 的导函数),若
的导函数),若
 ,则
,则 的大小关系是
的大小关系是
A. 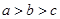 B.
B.  C.
C.  D.
D. 
【答案】
C
【解析】本试题主要是考查了抽象函数的奇偶性和单调性的判定和运用 。
因为已知函数y=f(x-1)关于(1,0)对称,故f(x)关于原点对称,同时当x<0,f(x)单调递减,那么y=xf(x)在小于零的区间上递减,并且利用f(x)是奇函数,得到y=xf(x)是偶函数,由于 ,那么根据图像的对称性和单调性可知结论为选c>a>b,选C.
,那么根据图像的对称性和单调性可知结论为选c>a>b,选C.
解决该试题的关键是判定y=xf(x)在小于零的区间上递减,并且利用f(x)是奇函数,得到y=xf(x)是偶函数。

练习册系列答案
相关题目
 上的函数
上的函数 ,有下述四个命题; ①若
,有下述四个命题; ①若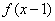 的图像关于点
的图像关于点 对称;②若对
对称;②若对 ,有
,有 ,则
,则 的图像关于直线
的图像关于直线 对称;③若函数
对称;③若函数 与函数
与函数 的图像关于直线
的图像关于直线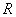 上的函数
上的函数 ,有下述四个命题;
,有下述四个命题; 的图像关于点
的图像关于点 对称;
对称; ,有
,有 ,则
,则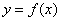 的图像关于直线
的图像关于直线 对称;
对称; 与函数
与函数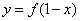 的图像关于直线
的图像关于直线 上的函数
上的函数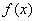 ,有下述四个命题; ①若
,有下述四个命题; ①若 的图像关于点
的图像关于点 对称;②若对
对称;②若对 ,有
,有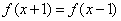 ,则
,则 的图像关于直线
的图像关于直线 对称;③若函数
对称;③若函数 与函数
与函数 的图像关于直线
的图像关于直线