题目内容
若a、b∈R，命题p：
＞
，命题q：a＜b＜0，则命题p是命题q成立的（ ）
| 1 |
| a |
| 1 |
| b |
分析：若
＞
可得b＞a＞0或a＜b＜0或a＞0＞b，从而可进行判断充分性与必要性
| 1 |
| a |
| 1 |
| b |
解答：解：若
＞
则
-
=
＞0
∴
或
即b＞a＞0或a＜b＜0或a＞0＞b
∴q⇒p，p推不出q
∴p是q成立的必要不充分条件
故选B
| 1 |
| a |
| 1 |
| b |
则
| 1 |
| a |
| 1 |
| b |
| b-a |
| ab |
∴
|
|
即b＞a＞0或a＜b＜0或a＞0＞b
∴q⇒p，p推不出q
∴p是q成立的必要不充分条件
故选B
点评：本题的考点是必要条件、充分条件与充要条件的判断，主要考查充要条件的问题．解答的关键是要准确求解分式不等式
练习册系列答案
相关题目
命题p：若a、b∈R，则|a|+|b|＞1是|a+b|＞1的充分而不必要条件；命题q：函数y=
的定义域是（-∞，-1]∪[3，+∞），则（ ）
| |x-1|-2 |
| A、“p或q”为假 |
| B、“p且q”为真 |
| C、p真q假 |
| D、p假q真 |
命题p：若a、b∈R，|a|+|b|＞1 则|a+b|＞1．
命题q：等轴双曲线
-
=1(a＞0，b＞0)中a=b．
则以上两个命题中（ ）
命题q：等轴双曲线
| x2 |
| a2 |
| y2 |
| b2 |
则以上两个命题中（ ）
| A、“p或q”为假 |
| B、“p且q”为真 |
| C、p真q假 |
| D、p假q真 |
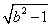；命题q：直线y=ax+b与圆x2+y2=1相交，则p是q的