题目内容
设函数f(x)=ax-1nx,
(1)若a=2,求函数f(x)的单调区间;
(2)若不等式f(x)>0恒成立,求a的取值范围.
解:(1)当a=2时,f(x)=2x-1nx,
∴f′(x)=2- =
=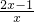 (x>0),
(x>0),
当0<x< ,f′(x)<0,f(x)=2x-1nx在(0,
,f′(x)<0,f(x)=2x-1nx在(0, )上单调递减;
)上单调递减;
当x> ,f′(x)>0,f(x)=2x-1nx在(
,f′(x)>0,f(x)=2x-1nx在( ,+∞)上单调递增;
,+∞)上单调递增;
∴函数f(x)的单调递减区间为(0, ),单调递增区间为(
),单调递增区间为( ,+∞);
,+∞);
(2)依题意,∵x>0,
f(x)=ax-1nx>0恒成立
?ax>lnx恒成立
?a> 恒成立
恒成立
?a>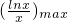 .
.
令g(x)= ,则g′(x)=
,则g′(x)= ,
,
当0<x<e,g′(x)>0,g(x)在(0,e)上单调递增;
当x>e,g′(x)<0,g(x)在(e,+∞)上单调递减;
∴g(x)max=g(e)= .
.
∴a> .
.
分析:(1)当a=2,f(x)=2x-1nx,可求得f′(x),利用导数即可判断函数f(x)的单调区间;
(2)将f(x)=ax-1nx>0恒成立转化为a> 恒成立,构造函数g(x)=
恒成立,构造函数g(x)= ,利用导数可求得g(x)max,从而求得a的范围.
,利用导数可求得g(x)max,从而求得a的范围.
点评:本题考查利用导数研究函数的单调性,考查函数恒成立问题,突出构造函数的应用,考查转化思想与分类讨论思想的运用,属于难题.
∴f′(x)=2-
 =
=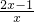 (x>0),
(x>0),当0<x<
 ,f′(x)<0,f(x)=2x-1nx在(0,
,f′(x)<0,f(x)=2x-1nx在(0, )上单调递减;
)上单调递减;当x>
 ,f′(x)>0,f(x)=2x-1nx在(
,f′(x)>0,f(x)=2x-1nx在( ,+∞)上单调递增;
,+∞)上单调递增;∴函数f(x)的单调递减区间为(0,
 ),单调递增区间为(
),单调递增区间为( ,+∞);
,+∞);(2)依题意,∵x>0,
f(x)=ax-1nx>0恒成立
?ax>lnx恒成立
?a>
 恒成立
恒成立?a>
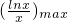 .
.令g(x)=
 ,则g′(x)=
,则g′(x)= ,
,当0<x<e,g′(x)>0,g(x)在(0,e)上单调递增;
当x>e,g′(x)<0,g(x)在(e,+∞)上单调递减;
∴g(x)max=g(e)=
 .
.∴a>
 .
.分析:(1)当a=2,f(x)=2x-1nx,可求得f′(x),利用导数即可判断函数f(x)的单调区间;
(2)将f(x)=ax-1nx>0恒成立转化为a>
 恒成立,构造函数g(x)=
恒成立,构造函数g(x)= ,利用导数可求得g(x)max,从而求得a的范围.
,利用导数可求得g(x)max,从而求得a的范围.点评:本题考查利用导数研究函数的单调性,考查函数恒成立问题,突出构造函数的应用,考查转化思想与分类讨论思想的运用,属于难题.

练习册系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |