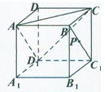
题目内容
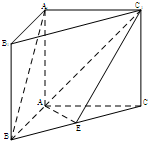
如图,四棱柱ABCD-A′B′C′D′中,侧棱与底面垂直,AB∥CD,AD⊥DC,且AB=AD=1,BC=
,AA′=
.
(I)求证:DB⊥BC′;
(II)求二面角A′-BD-C的大小.
| 2 |
| ||
| 2 |
(I)求证:DB⊥BC′;
(II)求二面角A′-BD-C的大小.

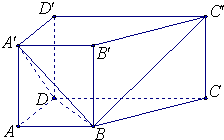
证明:(I)作BM⊥CD,垂足为M,连接AM.
因为AB∥CD,AD⊥DC,BM⊥CD,且AB=AD=1,
∴四边形ABMD是正方形
∴BM=DM=1,BD=
又∵BC=
,
∴CM=
=1
∴CD=2,即CD2=BD2+BC2
∴DB⊥BC,
又∵DB⊥B′B,B′B∩BC=B
∴DB⊥平面BC′
而BC′?平面BC′
∴DB⊥BC′
(II)设AM与BD交于点E,连接A′E
由(I)知,ME⊥BD,且DE=BE
∵A′A⊥平面ABCD,
∴A′A⊥AD,A′A⊥AB
又∵AB=AD=1,∴A′D=A′B
又∵DE=BE,
∴A′E⊥BD
综上可知∠A′EM即为二面角A′-BD-C的平面角,
在△A′AE中,∵A′A=
,AE=
BD=
∴tan∠A′EA=
=
即∠A′EA=60°
∴∠A′EM=120°
∴二面角A′-BD-C的大小为120°

因为AB∥CD,AD⊥DC,BM⊥CD,且AB=AD=1,
∴四边形ABMD是正方形
∴BM=DM=1,BD=
| 2 |
又∵BC=
| 2 |
∴CM=
| BC2-BM2 |
∴CD=2,即CD2=BD2+BC2
∴DB⊥BC,
又∵DB⊥B′B,B′B∩BC=B
∴DB⊥平面BC′
而BC′?平面BC′
∴DB⊥BC′
(II)设AM与BD交于点E,连接A′E
由(I)知,ME⊥BD,且DE=BE
∵A′A⊥平面ABCD,
∴A′A⊥AD,A′A⊥AB
又∵AB=AD=1,∴A′D=A′B
又∵DE=BE,
∴A′E⊥BD
综上可知∠A′EM即为二面角A′-BD-C的平面角,
在△A′AE中,∵A′A=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴tan∠A′EA=
| AA′ |
| AE |
| 3 |
即∠A′EA=60°
∴∠A′EM=120°
∴二面角A′-BD-C的大小为120°


练习册系列答案
相关题目
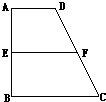 已知梯形ABCD中,AD
已知梯形ABCD中,AD