题目内容
如图,在平面有点A、B、P、Q,其中![]() ,
,![]() 设△APB与△PQB面积为S、T,求S2+T2的取值范围.
设△APB与△PQB面积为S、T,求S2+T2的取值范围.
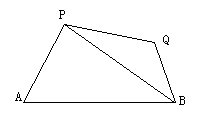
![]()
解析:
设∠BAP=α α∈[0,![]() ]
]
∠BQP=β,在△PAB,△PBQ中
由余弦定理cosβ=cosα-1
∴S2+T2=(![]() sinα)2+(
sinα)2+(![]() sinβ)2
sinβ)2
=-![]() (cos
(cos![]() -
-![]() )2+
)2+![]()
∴当cosα=1时,S2+T2有最小值![]()
当cosα=![]() 时,S2+T2有最大值
时,S2+T2有最大值![]()

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
题目内容
如图,在平面有点A、B、P、Q,其中![]() ,
,![]() 设△APB与△PQB面积为S、T,求S2+T2的取值范围.
设△APB与△PQB面积为S、T,求S2+T2的取值范围.
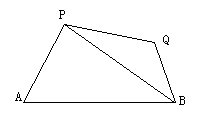
![]()
设∠BAP=α α∈[0,![]() ]
]
∠BQP=β,在△PAB,△PBQ中
由余弦定理cosβ=cosα-1
∴S2+T2=(![]() sinα)2+(
sinα)2+(![]() sinβ)2
sinβ)2
=-![]() (cos
(cos![]() -
-![]() )2+
)2+![]()
∴当cosα=1时,S2+T2有最小值![]()
当cosα=![]() 时,S2+T2有最大值
时,S2+T2有最大值![]()

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案