题目内容
 如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )
如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )分析:对于A,由于三棱锥A-A1BD为底面A1BD为正三角形的正棱锥,故H是△A1BD的垂心;
对于B,由正方体的性质可知,AC1⊥平面A1BD;
对于C,由于平面CB1D1∥平面A1BD,由AH⊥平面A1BD,可知C正确;
对于D,直线AH和BB1夹角就是直线AH和AA1夹角,计算即可判断其正误.
对于B,由正方体的性质可知,AC1⊥平面A1BD;
对于C,由于平面CB1D1∥平面A1BD,由AH⊥平面A1BD,可知C正确;
对于D,直线AH和BB1夹角就是直线AH和AA1夹角,计算即可判断其正误.
解答:解:依题意知,三棱锥A-A1BD为底面A1BD为正三角形的正棱锥,
∴H是△A1BD的中心,也是△A1BD的垂心,故A正确;
对于B,由于三棱锥C1-A1BD为底面A1BD为正三角形的正棱锥,
∴C1H⊥平面A1BD;
∴AH∥C1H,
又AH∩C1H=H,
∴A、H、C1三点共线,故B正确;
对于C,∵CD1∥BA1,B1D1∥BD,B1D1∩CD1=D1,BA1∩BD=B,
∴平面CB1D1∥平面A1BD,
又AH⊥平面A1BD,
∴AH⊥平面CB1D1,故C正确;
对于D,∵BB1∥AA1,
∴直线AH和BB1夹角就是直线AH和AA1夹角,设为θ,
设正方体的边长为a,在RT△AHA1中,AA1=a,A1H=
a×
×
=
a,
∴sinθ=
=
≠
,故D错误;
故选D.
∴H是△A1BD的中心,也是△A1BD的垂心,故A正确;
对于B,由于三棱锥C1-A1BD为底面A1BD为正三角形的正棱锥,
∴C1H⊥平面A1BD;
∴AH∥C1H,
又AH∩C1H=H,
∴A、H、C1三点共线,故B正确;
对于C,∵CD1∥BA1,B1D1∥BD,B1D1∩CD1=D1,BA1∩BD=B,
∴平面CB1D1∥平面A1BD,
又AH⊥平面A1BD,
∴AH⊥平面CB1D1,故C正确;
对于D,∵BB1∥AA1,
∴直线AH和BB1夹角就是直线AH和AA1夹角,设为θ,
设正方体的边长为a,在RT△AHA1中,AA1=a,A1H=
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| ||
| 3 |
∴sinθ=
| A1H |
| AA1 |
| ||
| 3 |
| ||
| 2 |
故选D.
点评:本题考查空间几何体线面垂直、面面平行、线面角,考查分析推理与运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2011•惠州模拟)如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )
(2011•惠州模拟)如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )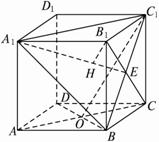
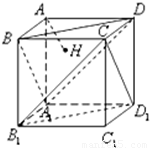 如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )
如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )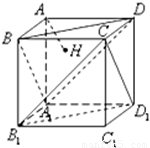 如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )
如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )