题目内容
函数f(x)=cos2x+sinx+1,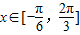 的值域为 .
的值域为 .
【答案】分析:将函数f(x)变为关于sinx的二次函数,再由二次函数的性质求函数的值域.
解答:解:由题意可得:y=-sin2x+sinx+2=-(sinx- )2+
)2+ ,
,
又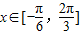 ,sinx∈[-
,sinx∈[- ,1]
,1]
当sinx= 时,函数f(x)取到最大值为
时,函数f(x)取到最大值为 ,
,
当sinx=- 时,函数f(x)取到最小值为
时,函数f(x)取到最小值为 ,
,
综上函数f(x)的值域是[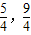 ].
].
故答案为[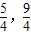 ].
].
点评:本题考查正弦函数的定义域和值域,求解本题关键是将函数变为关于sinx的二次函数,由配方法将本方,根据正弦函数的有界性判断出函数的最值,从而得出函数的值域,本题是三角函数求值域的题型中一个很重要的题型,其规律是转化为关于三角函数二次函数,将问题变为二次函数在闭区间上的最值问题.
解答:解:由题意可得:y=-sin2x+sinx+2=-(sinx-
 )2+
)2+ ,
,又
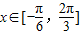 ,sinx∈[-
,sinx∈[- ,1]
,1]当sinx=
 时,函数f(x)取到最大值为
时,函数f(x)取到最大值为 ,
,当sinx=-
 时,函数f(x)取到最小值为
时,函数f(x)取到最小值为 ,
,综上函数f(x)的值域是[
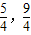 ].
].故答案为[
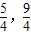 ].
].点评:本题考查正弦函数的定义域和值域,求解本题关键是将函数变为关于sinx的二次函数,由配方法将本方,根据正弦函数的有界性判断出函数的最值,从而得出函数的值域,本题是三角函数求值域的题型中一个很重要的题型,其规律是转化为关于三角函数二次函数,将问题变为二次函数在闭区间上的最值问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目