��Ŀ����
ij��������һ�ֲ�Ʒ�ijɱ��ѹ�����������ɣ���ԭ���Ϸ�ÿ��50Ԫ����ְ������֧��7500+20xԪ���۵�������������ȷ���Ϊx2��30x+600Ԫ������x�Ǹó��������ֲ�Ʒ���ܼ�����
��I����ÿ����Ʒ�ijɱ���p��x����Ԫ����ʾ�ɲ�Ʒ����x�ĺ���������ÿ����Ʒ����ͳɱ��ѣ�
��������ó����������ֲ�Ʒ������x������170������ȫ�����ۣ������г����飬ÿ����Ʒ�����ۼ�ΪQ��x����Ԫ������Q��x��=1240��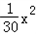 �������������ټ���Ʒ����������ߣ���������������������=�����۶�ܵijɱ���
�������������ټ���Ʒ����������ߣ���������������������=�����۶�ܵijɱ���
��I����ÿ����Ʒ�ijɱ���p��x����Ԫ����ʾ�ɲ�Ʒ����x�ĺ���������ÿ����Ʒ����ͳɱ��ѣ�
��������ó����������ֲ�Ʒ������x������170������ȫ�����ۣ������г����飬ÿ����Ʒ�����ۼ�ΪQ��x����Ԫ������Q��x��=1240��
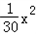 �������������ټ���Ʒ����������ߣ���������������������=�����۶�ܵijɱ���
�������������ټ���Ʒ����������ߣ���������������������=�����۶�ܵijɱ����⣺��I��P��x��=50+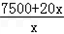 +
+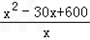 =
=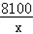 +x+40��
+x+40��
�ɻ�������ʽ��P��x����2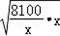 +40=220��
+40=220��
���ҽ���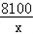 =x����x=90ʱ���Ⱥų�����
=x����x=90ʱ���Ⱥų�����
����P��x��=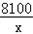 +x+40��ÿ����Ʒ����ͳɱ���Ϊ220 Ԫ��
+x+40��ÿ����Ʒ����ͳɱ���Ϊ220 Ԫ��
������������Ϊy=f��x��=xQ��x����xP��x��=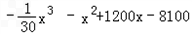 ��
��
f�䣨x��=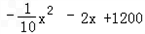 =
=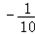 ��x��100����x+120��
��x��100����x+120��
��0��x��100ʱ��f�䣨x����0����x��100ʱ��f�䣨x����0��
����f��x���ڣ�0��100�������������ڣ�100��170�������ݼ���
���Ե�x=100ʱ��ymax=f��100��=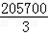
������100����Ʒʱ����������ߣ����������Ϊ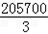 ��
��
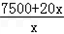 +
+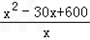 =
=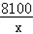 +x+40��
+x+40���ɻ�������ʽ��P��x����2
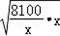 +40=220��
+40=220�����ҽ���
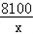 =x����x=90ʱ���Ⱥų�����
=x����x=90ʱ���Ⱥų���������P��x��=
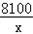 +x+40��ÿ����Ʒ����ͳɱ���Ϊ220 Ԫ��
+x+40��ÿ����Ʒ����ͳɱ���Ϊ220 Ԫ��������������Ϊy=f��x��=xQ��x����xP��x��=
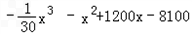 ��
��f�䣨x��=
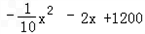 =
=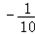 ��x��100����x+120��
��x��100����x+120����0��x��100ʱ��f�䣨x����0����x��100ʱ��f�䣨x����0��
����f��x���ڣ�0��100�������������ڣ�100��170�������ݼ���
���Ե�x=100ʱ��ymax=f��100��=
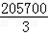
������100����Ʒʱ����������ߣ����������Ϊ
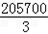 ��
��
��ϰ��ϵ�д�
�����Ŀ
 ij��������һ�ֲ�Ʒ�Ĺ̶��ɱ���20000Ԫ��ÿ����һ����Ʒ��Ҫ����Ͷ��100Ԫ���г����۲����е�����֪���г������ֲ�Ʒ����������Ϊ1000�������������뺯��
ij��������һ�ֲ�Ʒ�Ĺ̶��ɱ���20000Ԫ��ÿ����һ����Ʒ��Ҫ����Ͷ��100Ԫ���г����۲����е�����֪���г������ֲ�Ʒ����������Ϊ1000�������������뺯��