题目内容
已知函数![]() (a,c∈R,a>0,b是自然数)是奇函数,f(x)有最大值
(a,c∈R,a>0,b是自然数)是奇函数,f(x)有最大值![]() ,且f(1)>
,且f(1)>![]() .
.
(1)求函数f(x)的解析式;
(2)是否存在直线l与y=f(x)的图象交于P、Q两点,并且使得P、Q两点关于点(1,0)对称,若存在,求出直线l的方程,若不存在,说明理由.
(1)f(x)=![]() (2)P (
(2)P (![]() )或(
)或(![]() ),Q(
),Q(![]() )或Q(
)或Q(![]() ),过P、Q的直线l的方程: x–4y–1=0即为所求.
),过P、Q的直线l的方程: x–4y–1=0即为所求.
解析:
(1)∵f(x)是奇函数
∴f(–x)=–f(x),即
![]()
∴–bx+c=–bx–c ∴c=0
∴f(x)=![]()
由a>0,b是自然数得当x≤0时,f(x)≤0,
当x>0时,f(x)>0
∴f(x)的最大值在x>0时取得.
∴x>0时,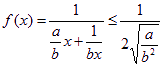
当且仅当![]()
即![]() 时,f(x)有最大值
时,f(x)有最大值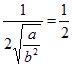
∴![]() =1,∴a=b2 ①
=1,∴a=b2 ①
又f(1)>![]() ,∴
,∴![]() >
>![]() ,∴5b>2a+2 ②
,∴5b>2a+2 ②
把①代入②得2b2–5b+2<0解得![]() <b<2
<b<2
又b∈N,∴b=1,a=1,∴f(x)=![]()
(2)设存在直线l与y=f(x)的图象交于P、Q两点,且P、Q关于点(1,0)对称,
P(x0,y0)则Q(2–x0,–y0),∴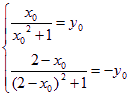 ,消去y0,得x02–2x0–1=0
,消去y0,得x02–2x0–1=0
解之,得x0=1±![]() ,
,
∴P点坐标为(![]() )或(
)或(![]() )
)
进而相应Q点坐标为Q(![]() )或Q(
)或Q(![]() ).
).
过P、Q的直线l的方程: x–4y–1=0即为所求.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
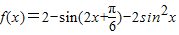 ,x∈R
,x∈R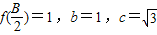 ,求a的值.
,求a的值. 定义在R上的奇函数,当
定义在R上的奇函数,当 时,
时, ,给出下列命题:
,给出下列命题: 时,
时, ②函数
②函数 的解集为
的解集为 ④
④ ,都有
,都有
 (k∈R),若函数
(k∈R),若函数 有三个零点,则实数k的取值范围是( )
有三个零点,则实数k的取值范围是( )