题目内容
已知函数f(x)=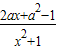 ,其中a∈R.
,其中a∈R.(1)若a=1时,记h(x)=
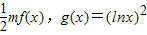 +2ex-2,存在x1,x2∈(0,1]使h(x1)>g(x2)成立,求实数m的取值范围;
+2ex-2,存在x1,x2∈(0,1]使h(x1)>g(x2)成立,求实数m的取值范围;(2)若f(x)在[0,+∞)上存在最大值和最小值,求a的取值范围.
【答案】分析:(1)a=1时,存在x1,x2∈(0,1]使h(x1)>g(x2)成立,等价于h(x)max>g(x)min,利用导数、函数单调性可求得两函数的最值;
(2)f′(x)=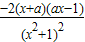 ,按照a=0,a>0,a<0三种情况进行讨论,根据单调性可判断函数最值情况;
,按照a=0,a>0,a<0三种情况进行讨论,根据单调性可判断函数最值情况;
解答:解:(1)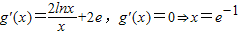 ,
,
x∈(0,e-1),g'(x)<0,g(x)递减;x∈(e-1,1),g'(x)>0,g(x)递增,
∴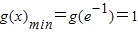 ,∴h(x)=
,∴h(x)=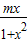 ,
,
显然m>0,则h(x)在(0,1]上是递增函数,h(x)max=m,
∴m>1,
所以存在x1,x2∈(0,1]使h(x1)>g(x2)成立时,实数m的取值范围是(1,+∞);
(2)解:f′(x)=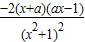 ,
,
①当a=0时,f′(x)=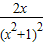 .
.
所以f(x)在(0,+∞)上单调递增,在(-∞,0)上单调递减,f(x)在[0,+∞)上不存在最大值和最小值;
当a≠0,f(x)=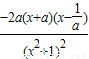 ,
,
②当a>0时,令f'(x)=0,得x1=-a<0,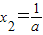 ,f(x)与f'(x)的情况如下:
,f(x)与f'(x)的情况如下:
故f(x)的单调减区间是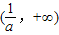 ;单调增区间是
;单调增区间是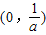 .
.
当a>0时,由上得,f(x)在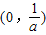 单调递增,在
单调递增,在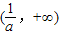 单调递减,
单调递减,
所以f(x)在(0,+∞)上存在最大值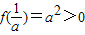 .
.
又因为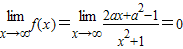 ,
,
设x为f(x)的零点,易知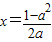 ,且
,且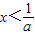 .从而x>x时,f(x)>0;x<x时,f(x)<0.
.从而x>x时,f(x)>0;x<x时,f(x)<0.
若f(x)在[0,+∞)上存在最小值,必有f(0)≤0,解得-1≤a≤1.
所以a>0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(0,1].
③当a<0时,f(x)与f'(x)的情况如下:
所以f(x)的单调增区间是(-a,+∞);单调减区间是(0,-a),f(x)在(0,-a)单调递减,在(-a,+∞)单调递增,
所以f(x)在(0,+∞)上存在最小值f(-a)=-1.
又因为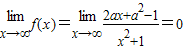 ,
,
若f(x)在[0,+∞)上存在最大值,必有f(0)≥0,解得a≥1,或a≤-1.
所以a<0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(-∞,-1].
综上,a的取值范围是(-∞,-1]∪(0,1].
点评:本题考查利用导数研究函数的单调性、最值等知识,考查学生综合运用所学知识分析问题解决问题的能力,综合性强,难度大,能力要求较高.
(2)f′(x)=
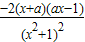 ,按照a=0,a>0,a<0三种情况进行讨论,根据单调性可判断函数最值情况;
,按照a=0,a>0,a<0三种情况进行讨论,根据单调性可判断函数最值情况;解答:解:(1)
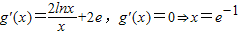 ,
,x∈(0,e-1),g'(x)<0,g(x)递减;x∈(e-1,1),g'(x)>0,g(x)递增,
∴
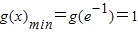 ,∴h(x)=
,∴h(x)=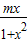 ,
,显然m>0,则h(x)在(0,1]上是递增函数,h(x)max=m,
∴m>1,
所以存在x1,x2∈(0,1]使h(x1)>g(x2)成立时,实数m的取值范围是(1,+∞);
(2)解:f′(x)=
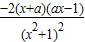 ,
,①当a=0时,f′(x)=
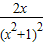 .
.所以f(x)在(0,+∞)上单调递增,在(-∞,0)上单调递减,f(x)在[0,+∞)上不存在最大值和最小值;
当a≠0,f(x)=
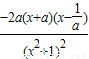 ,
,②当a>0时,令f'(x)=0,得x1=-a<0,
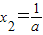 ,f(x)与f'(x)的情况如下:
,f(x)与f'(x)的情况如下:| x | (0,x2) | x2 | (x2,+∞) |
| f'(x) | + | - | |
| f(x) | ↗ | f(x2) | ↘ |
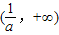 ;单调增区间是
;单调增区间是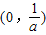 .
.当a>0时,由上得,f(x)在
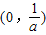 单调递增,在
单调递增,在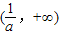 单调递减,
单调递减,所以f(x)在(0,+∞)上存在最大值
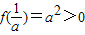 .
.又因为
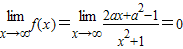 ,
,设x为f(x)的零点,易知
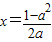 ,且
,且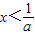 .从而x>x时,f(x)>0;x<x时,f(x)<0.
.从而x>x时,f(x)>0;x<x时,f(x)<0.若f(x)在[0,+∞)上存在最小值,必有f(0)≤0,解得-1≤a≤1.
所以a>0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(0,1].
③当a<0时,f(x)与f'(x)的情况如下:
| x | (0,x1) | x1 | (x1,+∞) |
| f'(x) | - | + | |
| f(x) | ↘ | f(x1) | ↗ |
所以f(x)在(0,+∞)上存在最小值f(-a)=-1.
又因为
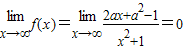 ,
,若f(x)在[0,+∞)上存在最大值,必有f(0)≥0,解得a≥1,或a≤-1.
所以a<0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(-∞,-1].
综上,a的取值范围是(-∞,-1]∪(0,1].
点评:本题考查利用导数研究函数的单调性、最值等知识,考查学生综合运用所学知识分析问题解决问题的能力,综合性强,难度大,能力要求较高.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|