题目内容
函数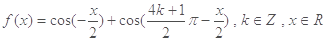 .
.
(1)求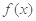 的周期;
的周期;
(2)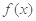 在
在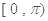 上的减区间;
上的减区间;
(3)若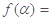
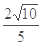 ,
,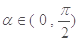 ,求
,求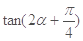 的值.
的值.
(1)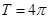 ;(2)
;(2) 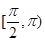 ;(3)
;(3) 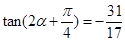 .
.
解析试题分析:(1)先利用三角函数的诱导公式将函数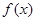 化为
化为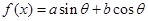 形式,再利用辅助角公式将其化为
形式,再利用辅助角公式将其化为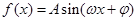 的形式,则周期公式
的形式,则周期公式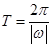 可求得周期.
可求得周期.
(2)先将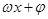 看成一个整体,由
看成一个整体,由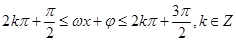 解得正弦函数的减区间,再取
解得正弦函数的减区间,再取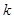 值,可求得函数
值,可求得函数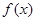 在
在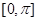 上的减区间.
上的减区间.
(3)将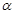 代入(1)中的解析式可求得
代入(1)中的解析式可求得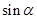 的值,又因为
的值,又因为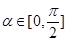 ,根据同角三角函数的基本关系式
,根据同角三角函数的基本关系式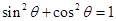 、
、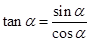 可求得
可求得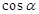 、
、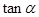 的值,再根据两角和的正切公式
的值,再根据两角和的正切公式 、二倍角公式
、二倍角公式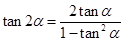 可求得
可求得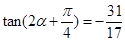 .
.
试题解析:(1)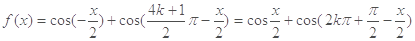
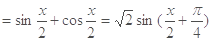 ,(
,(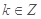 ), 所以
), 所以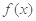 的周期
的周期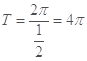 .
.
(2)由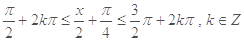 ,得
,得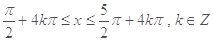 .
.
又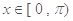 ,令
,令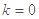 ,得
,得
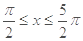 ;令
;令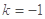 ,得
,得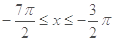 (舍去)
(舍去)
∴ 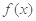 在
在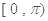 上的减区间是
上的减区间是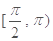 .
.
(3)由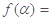
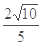 ,得
,得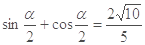 ,∴
,∴ 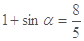 , ∴
, ∴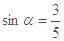
又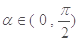 ,∴
,∴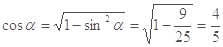
∴ 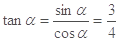 ,∴
,∴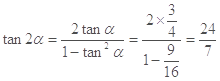
∴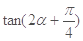
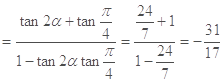 .
.
考点:1、三角函数的诱导公式、辅助角公式、同角三角函数的基关系式、两角和差公式、二倍角公式;2、三角函数的性质周期性、单调性.

练习册系列答案
相关题目
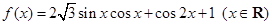 .
.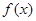 的最小正周期;
的最小正周期;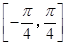 上的最小值,并写出
上的最小值,并写出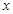 值.
值.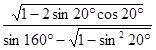 ;
;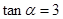 ,求
,求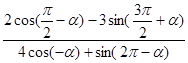 的值.
的值. .
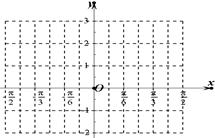
.
 的最小值及取最小值时
的最小值及取最小值时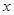 的集合;
的集合;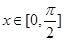 时的值域;
时的值域;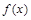 在区间
在区间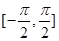 上的图像(要求列表,描点).
上的图像(要求列表,描点).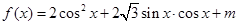 .其中
.其中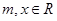
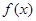 的最小正周期;
的最小正周期;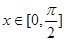 时,求实数
时,求实数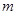 的值,使函数
的值,使函数 并求此时
并求此时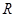 上的对称中心.
上的对称中心.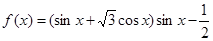 .
. 的单调递减区间;
的单调递减区间;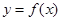 的图像向左平移
的图像向左平移 个单位,再将得到的图像横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图像横坐标变为原来的2倍(纵坐标不变)后得到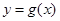 的图像,若
的图像,若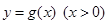 的图像与直线
的图像与直线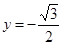 交点的横坐标由小到大依次是
交点的横坐标由小到大依次是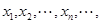 求数列
求数列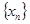 的前2n项的和。
的前2n项的和。 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9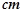 和15
和15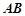 的顶部
的顶部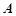 看建筑物
看建筑物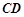 的视角
的视角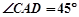 .
.
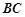 的长度;
的长度;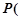 点
点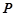 与点
与点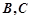 不重合),从点
不重合),从点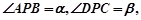 问点
问点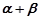 最小?
最小?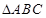 中,角
中,角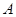 、
、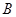 、
、 所对的边分别为
所对的边分别为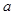 、
、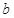 、
、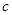 ,
,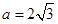 ,
,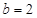 ,
,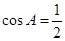 .
.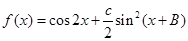 ,求函数
,求函数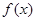 的单调递增区间.
的单调递增区间.